


Next: About this document ...
Note on Paramodulation
Here's a better description of the paramodulation rule we talked about
in class. Let
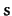 ,
, 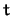 , and
, and 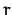 be terms
be terms
![$\gamma[r]$](img4.png) be a (possibly negated) literal that contains term
be a (possibly negated) literal that contains term 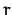 as
a subexpression
as
a subexpression
-
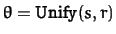 , and
, and
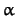 and
and 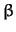 be (possibly empty) sets of literals.
be (possibly empty) sets of literals.
Then, given a clause
and another clause
you may conclude
Here's an example. Given
and
we can conclude
by setting 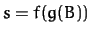 ,
, 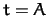 ,
, 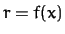 ,
,
![$\gamma[\cdot] =
p(h(\cdot))$](img17.png) , and
, and
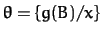 .
.
Michael G. Ross
2001-03-09