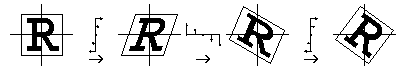
The technique of using three consecutive shears to rotate a 2-D image---illustrated by the following diagram---has been known for a while.
For 3-D images, there is an obvious nine-shear solution, obtained by
treating the 3-D rotation as the product of three 2-D rotations. Our
algorithm, which uses only three shears, is a sizable improvement over
that bound, and is actually the best that can be attained---just two shears
won't do. The algorithm, illustrated by the following figure,
proceeds much as in the two-dimensional case. Namely, a rotation
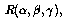where
are the
rotation's Euler angles, is decomposed as the product of three shears
.
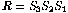Each of the three shears
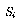is given by matrix of the form
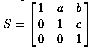(or a transpose of this form)
and is thus characterized by three real parameters (rather than just one as
in the two-dimensional case), which are in turn functions of the Euler angles.
This result may be stated more abstractly as a linear algebra identity. In
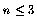dimensions, any orthogonal matrix
can be written in the form
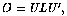, where
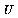and
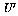are upper triangular matrices and
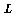is a
lower triangular matrix---all three matrices having all 1's along the
main diagonals. The question of whether this identity generalizes to
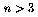is still open.