Macroscopic order from reversible lattice growth
models
Raissa M. D'Souza and Norman H. Margolus
The Problem:
We seek to understand mechanisms for the emergence of large scale
macroscopic order from local invertible microscopic dynamics.
Motivation:
Pattern formation is an intrinsically dissipative process, however
the laws of physics are microscopically reversible: there is no
dissipation at the microscopic scale. We are interested in simple systems
which organize into patterns through microscopically reversible dynamics.
They model how dissipation arises (i.e., how information flows between the
macroscopic and the microscopic degrees of freedom), and provide a clear
example of how to reconcile the macroscopic irreversibility that gives rise
to patterns with the microscopic reversibility adhered to by physical
processes. Aside from providing a laboratory in which to probe the
thermodynamics of pattern formation, implementations of reversible
microscopic models, and the understanding of invertible dynamics in
general, have technological significance, as discussed below.
Previous Work:
A review of the limited amount of previous work on reversible
microscopic models can be found in Ref.[1]. Several of
the models discussed therein use techniques introduced
to study reversible dynamics of spin systems on a lattice[2].
Previous work explicitly in the field of pattern formation
has focused on irreversible microscopic mechanisms, with examples
ranging from crystal growth, to Turing patterns in chemical reactions,
to patterns formed by growing bacterial colonies[3].
Approach:
We build models which attempt to capture aspects of classical physics:
the models are local, deterministic, have exact conservations, and
are exactly microscopically reversible.
We implement the models as lattice gas cellular
automata, on a special purpose cellular automata machine, the
CAM8[4] (which was developed here at MIT in the course of
the past decade). The analysis of the models relies primarily on
the standard techniques of statistical mechanics, which enables the
prediction of macroscopic quantities through a statistical analysis
of the microscopic details of the system. In some cases we can also
directly take the continuum limit of the discrete, microscopic dynamics
to establish the partial differential equations obeyed in the macroscopic
limit for the system.
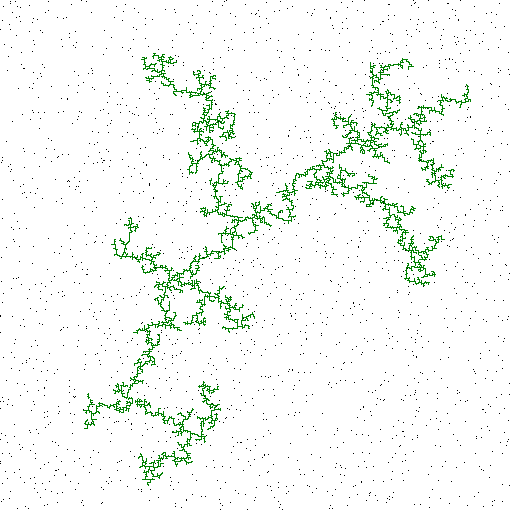 (a)
(a)
 (b)
(b)
(a) A typical equilibrium cluster generated by the RA model.
This cluster has undergone a transition from a dense bushy morphology
to the branched polymer shown above. (b) The asymptotic state
of the three-dimensional SAME rule. We render a cross section
through the center of the space. This is a
stable, dynamical structure: there are small microscopic fluctuations
at each time step, yet the macroscopic structure will persist
for longer than we could possibly observe it.
Two interesting systems we are concurrently studying are the
Reversible Aggregation (RA) model and the three-dimensional
SAME model. The first model is of cluster growth via the
diffusive aggregation of particles in a closed system.
The particles release latent heat into a heat bath upon aggregating,
while singly connected cluster members can absorb heat and evaporate.
Initially the heat bath is empty, so aggregation events happen more
readily than evaporation. The heat bath quickly reaches a steady state,
meaning the system now has a well defined temperature, and that the
net number of aggregation and evaporation events are equal. The growth
morphology of the cluster correspondingly undergoes a transition
from the typical ``frost on a window pane'' pattern observed for
irreversible models of diffusive cluster growth[5], to the highest
entropy macrostate allowed for a connected cluster in a finite volume,
a branched polymer. We have studied the thermodynamics of this model
extensively, as well as quantifying the transition in the resulting
growth morphology via the fractal dimension of the clusters[6].
The second model, the three-dimensional SAME model, provides a
nice example of the emergence of large scale order with no
explicit entropy sink (i.e., no heat bath).
The model is a generalization of the dynamical Ising
model[2] of binary spins on a lattice which interact with nearest
neighbor sites. The system evolves so as to maximize the entropy. In
the analogous two dimensional dynamics we observe this system evolve
from a small block of randomness in a uniform background to a
completely random and disordered state. In contrast, in three dimensions
the system evolves from a small cube of randomness to a stable dynamical
structure with long range order resembling a square pyramid
embedded in fluctuating spherical shells.
Discrete systems have a finite, but extremely large, number of distinct
microscopic states. In general, reversible systems visit almost all of
the states before cycling back to the initial state, thus the stable
structure generated by the SAME model will persist for longer
than we could ever possibly observe it. A general discussion of this
model and of cycle times in discrete reversible systems appears in
Ref.[1], a detailed discussion will appear in the soon to be
released thesis of the first author.
Difficulty:
The primary difficulty we encounter is trying to incorporate
more physics into our models---the constraints of locality, exact
conservation, and invertibility can be hard to reconcile with an
interesting macroscopic dynamics. We would also like to
analyze the macroscopic dynamics of physics-like discrete systems
using the language of physics. This would require the formulation of the
least action principle and the Euler-Lagrange equations for
discrete systems. By studying simple models we hope to gain insights
useful for dealing with this more general issue.
Impact:
Understanding the mechanisms of pattern formation has
obvious significance. By modeling the entire process of pattern
formation, including the dissipation, we hope to emulate
the mechanisms of nature much more accurately than do irreversible
models. The development of invertible dynamics and algorithms
has further technological significance such as pushing down the
barrier to atomic scale computing. Each bit of information erased
during a computation releases heat into the environment. Heat is
created in proportion to the volume of the computer, yet heat
leaves the computer only in proportion to the surface area. Hence, as
logic gate density in computers increases, the use of an invertible
dynamics (which does not erase information and hence does not need to produce
heat) will be required to keep the mechanical parts from burning up.
If we are to succeed in building quantum computers they too will require
invertible microscopic algorithms, as the laws of quantum mechanics
are unitary (and hence microscopically reversible).
Research Support:
Support for this research was provided by
the DARPA Reversible Computing Project, contract number
DABT63-95-C-0130.
References:
[1] N. H. Margolus, "Crystalline Computation", in Feynman and
Computation, Addison-Wesley, 1998.
[2] M. Creutz, "Deterministic Ising Dynamics", Annals of
Physics 167, 1986.
[3]A. L. Barabasi and U. E. Stanley, Fractal Concepts in Surface
Growth, Univ. of Cambridge Press, New York, 1995; J. E. Pearson,
"Complex Patterns in a Simple System", Science 261, 1993.;
E. Ben-Jacob et al.,"Response of bacterial colonies to
imposed anisotropy", Physical Review E 53, 1996.
[4] N. H. Margolus, "CAM-8: a computer architecture based on cellular
automata", in Pattern Formation and Lattice-Gas Automata,
American Mathematical Society, 1996.
[5] T. A. Witten and L. M. Sander,"Diffusion-Limited Aggregation: a
kinetic critical phenomenon",Physical Review Letters 47,
1981.
[6] R. M. D'Souza and N. H. Margolus,"Reversible aggregation in a
lattice gas model using coupled diffusion fields",submitted to
Physical Review E, 1998. (a)
(a)
 (b)
(b)
 (a)
(a)
 (b)
(b)