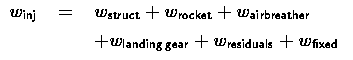 1
1A propellant transfer spaceplane is an aerodynamic space vehicle that uses a tanker to reduce the required takeoff gross weight and thus the weight of landing gear, thermal protection systems, wing, and so on. The objective is to enable HTHL spaceflight without resort to unsafe flying practices and ultra-advanced technology.
Let the injected weight of the aircraft, winj be given by:
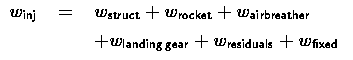 1
1
where:
wstruct = the weight of the structure, control surfaces, thermal protection system, tankage, etc.
wrocket = the weight of the rocket engines
wairbreather = the weight of the airbreathing engine, if any
wlanding gear = the weight of the landing gear
wresiduals = the weight of the unburnt propellant
wfixed = the scale independent weights: crew, payload, crew accommodations, subsystems
From the rocket equation, the initial weight w0 is given by:
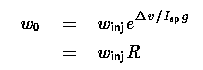 2
2
for which the Delta-v is the velocity change including all loss mechanisms, including back pressure, and the Isp is the vacuum specific impulse. Similarly, the propellant weight wprop is merely w0 - winj, or:
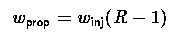 3
3
Let us write expressions for each of the terms in equation 1.
For the structural weight, we need to define a technology parameter t, which is the pounds per square foot of (structural weight + thermal protection system weight). For all-metal aerospaceplanes such as Boeing's RASV design, t is about 4.5 lb/ft2. For a composite structure with direct bonded tiles and a non-cryogenic dense propellant inside, t can be as low as 2.5 lb/ft2, just to define the range of plausible values. This argument contains an implicit assumption that the weight depends more on area than on volume. This is more or less the same as saying that the propellants are dense.
Further, we need to define a shape variable s, which is the ratio of wetted area to reference area. A theoretical 2D flat plate wing has s of 2.0, a B-2 is close to 2.2, a Boeing B-47 is about 8, and a well-blended wing-body such as the Avro Vulcan Bomber is about 2.8.
Finally, we need to have symbols for the dynamic pressure q (in lb/ft2) and the lift coefficient cL, so that we can equate the lift to the weight of the aircraft at tanker disconnect, which is the structural and aerodynamic "worst-case" condition. From this, we can write:
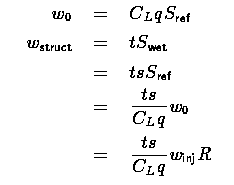 4
4
The rocket engine is sized by the required initial acceleration v and the rocket thrust to weight ratio r:
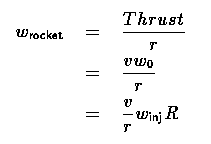 5
5
It must be noted that the choice of initial acceleration is a strong driver of Delta-v. It is also important to reference the thrust and r to the same condition: sea level, vacuum, or whatever, as long as it is consistent. Using tanker disconnect figures is preferred.
The airbreathing engine thrust to weight ratio j must be referenced to the tanker disconnect condition and include installation effects. Thus the thrust will be lower and the weight higher than the sea level static numbers you look up in an engine book or in Jane's. The condition for the airbreather is that if it is present it must be able to sustain the vehicle in level flight behind the tanker, and hence its thrust must be equal to the drag the vehicle sees at disconnect. As a result,
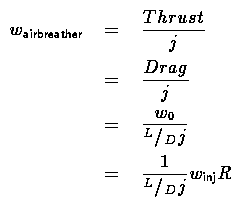 6
6
An important note is to make sure that the value of cL in equation 4 is compatible with the value of lift to drag ratio in equation 6, so that both equations are referenced to the same point in the aero database for the aircraft.
Landing gear weights are traditionally parameterized as a percentage l of the landed weight, varying between 2 and 3 percent. The landed weight of a propellant transfer spaceplane should be the takeoff weight, which consists of the injected weight, the weight of the fuel (not the oxidizer), and the weight of whatever additional propellant is needed to climb and rendezvous with the tanker and to stay on the tanker during the transfer. This is a pretty complicated calculation, so to simplify matters, we will say that the takeoff weight is a percentage p of the gross weight leaving the tanker, and revise the figure during detailed design based on real knowledge of the aerodynamics, propulsion, and propellant transfer system. The higher the mixture ratio between oxidizer and fuel, and the more airbreathing is done on the way to the tanker, the lower the value of p.
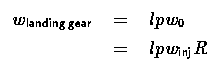 7
7
The final component of scale-dependent weight is the propellant residuals, which are routinely expressed as a fraction f of the loaded propellant (typically between 0.5 and 1 percent):
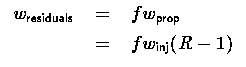 8
8
We can now write equation 1 in terms of equations 4 through 8, as:
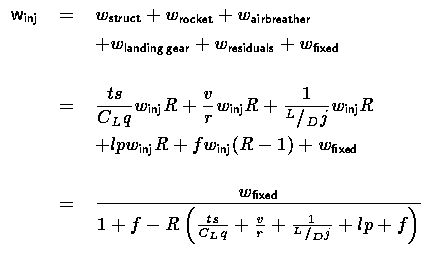 9
9
For the current Black Horse design, for example:
| t | 4 | lb/ft2 | j | n/a | -- |
|---|---|---|---|---|---|
| s | 2.8 | -- | l | 2% | -- |
| cL | 0.9 | -- | p | 28.1% | -- |
| q | 397.16 | lb/ft2 | f | 0.5% | -- |
| v | 1.4 | -- | Delta-v | 26,377 | ft/s |
| r | 75 | -- | Isp | 328 | s |
| L/D | n/a | -- | R | 12.18 | -- |
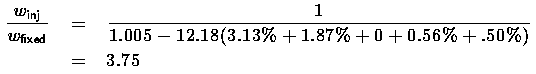 10
10
If the oxidizer weight is constrained by KC-135 tanker capacity (150,000 lbs) and offload rate (1500 gal/min -- KC-10 spec), then the total propellant available for consumption at an oxidizer:fuel mixture ratio of 7.25 is 145,070 lb (assuming the aircraft retains at disconnect 85% of the offloaded propellant). This implies a gross weight after disconnect of 158,050 lbs and an injected weight of 12,981 lbs. From equation 10, the maximum fixed weight is 3,447 lbs. Taking an avionics and subsystems weight of 1,200 lbs and a crew and crew systems weight of 1,000 lbs, the net payload is about 1,247 lbs.
The next step would of course be actually to design the vehicle, verify the assumptions, run a trajectory and sizing code, and iterate. It is important to check for the ability to enclose the required propellant volume, especially for small vehicles. The technique described here is only meant to allow the designer to "rough in" the trade space for a propellant transfer spaceplane.
For example, examining equation 10 reveals that the dominant parameter is structural weight, followed by engine, landing gear, and residuals. Descending to lower altitudes, smoothing and blending the design, operating at higher lift coefficient, or using more advanced structural technology will all reduce structural weight. In a similar way, investments in lightweight engines and landing gear can drive the remaining terms lower.
Let's add a turbofan engine to the vehicle:
| t | 4 | lb/ft2 | j | 4.5 | -- |
|---|---|---|---|---|---|
| s | 2.8 | -- | l | 2% | -- |
| cL | 0.9 | -- | p | 28.1% | -- |
| q | 397.16 | lb/ft2 | f | 0.5% | -- |
| v | 1.4 | -- | Delta-v | 26,377 | ft/s |
| r | 75 | -- | Isp | 328 | s |
| L/D | 5.8 | -- | R | 12.18 | -- |
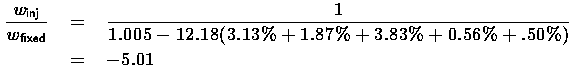 11
11
Notice that the airbreathing engine is now the single dominant mass component, and that the negative number shows that the problem is unsolvable as stated.
On the other hand, some airbreathing thrust can reduce the required rocket engine mass. Reducing lift coefficient somewhat can increase L/D. Operating the turbofan in parallel with the rocket can increase overall Isp for at least the first few Mach numbers. If we back the value of v off to 1.0, what value of Isp is needed to do at least as well as Black Horse?
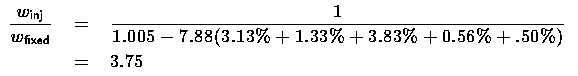 12
12
A mass ratio of 7.88 implies an Isp of 397 s, which even a low SFC turbofan is not going to be able to deliver in conjunction with a rocket.
If, however, one were to develop a fan-ramjet engine, such as that proposed by Kaiser-Marquardt, the value of j would be about 10, because of the lower inherent mass of the engine. Also, the engine could run at Mach numbers up to 4.5. Finally, we can examine a vehicle based on LO2 and Kerosene to take advantage of the high thrust to weight NK-43 engine, which delivers 330,000 lbs of thrust at 30,000 ft from a 3300 lb installation at a vacuum specific impulse of 346.3. Examining this case:
| t | 4 | lb/ft2 | j | 10 | -- |
|---|---|---|---|---|---|
| s | 2.8 | -- | l | 2% | -- |
| cL | 0.9 | -- | p | 28.1% | -- |
| q | 397.16 | lb/ft2 | f | 0.5% | -- |
| v | 1.0 | -- | Delta-v | 26,377 | ft/s |
| r | 100 | -- | Isp | 346.3 | s |
| L/D | 5.8 | -- | R | 10.67 | -- |
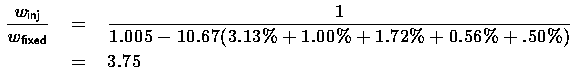 13
13
For this case, the conclusion is that a LO2/Kerosene vehicle based around a fan-ramjet engine and a single NK-43 has performance equivalent to Black Horse assuming no improvement in specific impulse from the airbreathing engine. The gross weight for this case is 330,000 lbs, the empty weight is 30,929 lbs, the fixed weight is 8,250 lbs, and the payload is about 6,000 lbs assuming the same avionics and crew systems weights as above.
If we assume that the airbreathing engine, contributing partial thrust up to Mach 4.5, allows the vehicle to average 370 sec of Isp, the technology level can decline a great deal for the same performance:
| t | 5.44 | lb/ft2 | j | 10 | -- |
|---|---|---|---|---|---|
| s | 2.8 | -- | l | 2% | -- |
| cL | 0.9 | -- | p | 28.1% | -- |
| q | 397.16 | lb/ft2 | f | 0.5% | -- |
| v | 1.0 | -- | Delta-v | 26,377 | ft/s |
| r | 100 | -- | Isp | 346.3 | s |
| L/D | 5.8 | -- | R | 10.67 | -- |
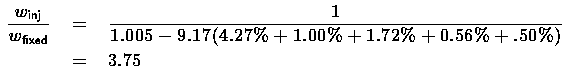 14
14
representing a 36% increase in required structural mass and a payload of 7,400 lbs.
Finally, let's assume a Vulcan-style configuration (L/D = 15 at cL = 0.6), the latest in structural technology (t=2.8), and the same engines as before. The net payload is 14,100 lbs in this case.
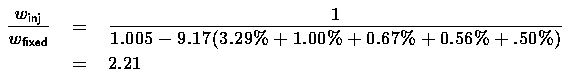 15
15