Abstract: In this work, we propose a methodology
for automatically correcting the spherical topology of any segmentation
under any digital connectivity.
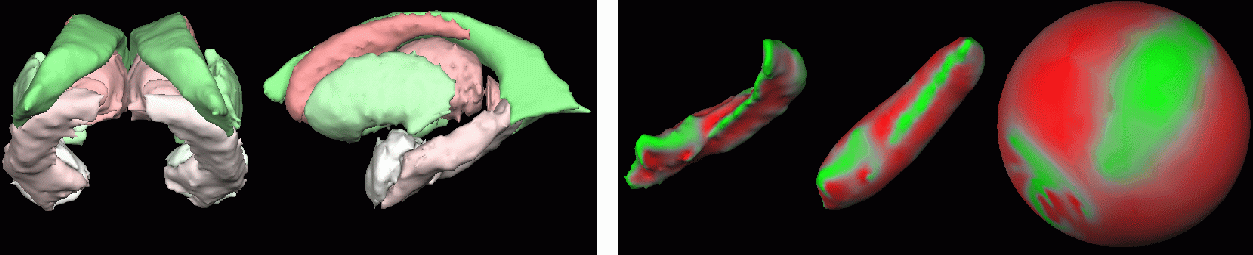
In an initial work (MICCAI 2003), a multiple region growing process, concurrently acting on the foreground and the background, divides the segmentation into connected components and successive minimum cost decisions guarantee convergence to correct spherical topology. In contrast to existing procedures that suppose specific initial segmentation (full connectivity, no cavities... ) and are designed for a particular task (cortical representation), no assumption is made on the initial image. Our method applied to subcortical segmentations allows us to correct the topology of fourteen deep nuclei in less than a minute (see figure below).
In an initial work (MICCAI 2003), a multiple region growing process, concurrently acting on the foreground and the background, divides the segmentation into connected components and successive minimum cost decisions guarantee convergence to correct spherical topology. In contrast to existing procedures that suppose specific initial segmentation (full connectivity, no cavities... ) and are designed for a particular task (cortical representation), no assumption is made on the initial image. Our method applied to subcortical segmentations allows us to correct the topology of fourteen deep nuclei in less than a minute (see figure below).
We are currently investigating different extensions
by integrating statistical and geometrical information into the localization
and the correction of the topological defects. We have introduced the
concept of "multisimple" point, which facilitates the merging of multiple
digital regions under topological constraints. With the help of this
new concept, we are currently developping different approaches. (topological
watershed techniques, multi-lesetset topology correction (see [1]) ),
phrased within a general Bayesian framework. This general approach is
appropriate to the topology correction of more complex structures, such
as the cortex.
Methods:
Excluding pathological cases, most subcortical brain
structures are fully connected and do not possess any topological artifact
such as handles or cavities: they have the simple topology of a sphere.
Many recent segmentation algorithms are able to identify and precisely
locate these structures, although without constraining the topology.
Being able to achieve accurate and topologically correct representation
of different brain structures is certainly of valuable interest in Medical
Imaging (Shape Analysis, Visualization...)
Our approach uses classical results of digital topology (see the work of G. Bertrand for more details [2]). We have introduced the concept of 'multisimple' point (see corresponding publications for more details), which allows us to concurrently work on different parts of the digital object, but still control the whole topology of the resulting segmentation. This digital concept is particularly usefull for multiple region growing techniques (watershed, multi-levelsets).
Similarly to the approaches developed by Han et al. (see [3]) and Kriegeskorte and Goeble (see [4]), we segment the initial digital volume So (the foreground object and its inverse object : the background) into a set of connected components (body components of known topology and residual components - see figure below) and build two interacting connected graphs. Schematically, the topology correction amounts to finding the components that should be deleted, i.e. added to the invese object. Using a Bayesian framework (we search for the map estimate of p(S|I) where S and I represent the estimated digital segmentation and the original M.R.Image respectively), iterative minimal graph decisions correct the topology of the binary volume and convergence is guaranteed.
Our approach uses classical results of digital topology (see the work of G. Bertrand for more details [2]). We have introduced the concept of 'multisimple' point (see corresponding publications for more details), which allows us to concurrently work on different parts of the digital object, but still control the whole topology of the resulting segmentation. This digital concept is particularly usefull for multiple region growing techniques (watershed, multi-levelsets).
Similarly to the approaches developed by Han et al. (see [3]) and Kriegeskorte and Goeble (see [4]), we segment the initial digital volume So (the foreground object and its inverse object : the background) into a set of connected components (body components of known topology and residual components - see figure below) and build two interacting connected graphs. Schematically, the topology correction amounts to finding the components that should be deleted, i.e. added to the invese object. Using a Bayesian framework (we search for the map estimate of p(S|I) where S and I represent the estimated digital segmentation and the original M.R.Image respectively), iterative minimal graph decisions correct the topology of the binary volume and convergence is guaranteed.
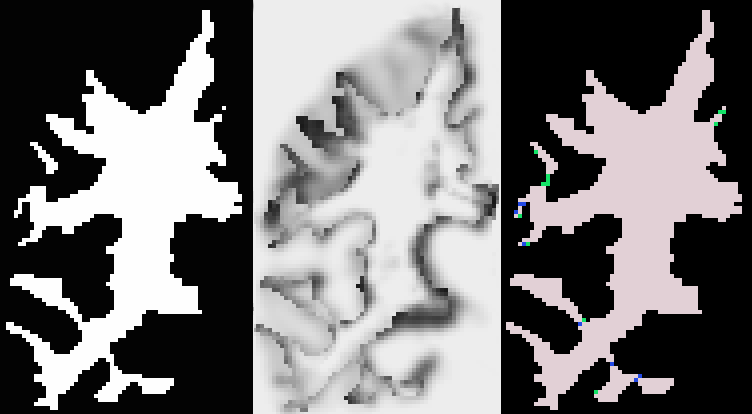
The initial binary segmentation S, its joint probability map p(I,S) , and the resulting segmentation into connected components
residual components are in green and blue - body components are in pink and black).
The novelty of our approach comes from the
fact that any initial segmentation (disconnected regions, handles,
cavities or holes) will still be corrected. No assumption is made about
the initial segmentation, and spherical topology is achieved under any
choice of digital topology. A Bayesian framework allows us to integrate
statistical information into the topology correction; topologically constrained
levelsets (introduced by Han et al. in [1]) associated with the concept
of multisimple point allow us to naturally integrate geometrical information
(curvature) and to silmutaneously correct different locations of the initial
volume.
Preliminary Results and Future work:
We have implemented a preliminary version of the
proposed method, based on previous work (MICCAI 2003).
In order to validate the proposed algorithm, we have apply our method to 25 brain segmentations, manually and automatically labeled. The Whole Brain Segmentation algorithm proposed by Fischl et al. in [5] was used to generate automatic brain segmentations and to generate the joint probabilities p(I(x),S(x)) for all voxels x. The pair of compatible digital connectivities that we use for all the experiences was (6,18).
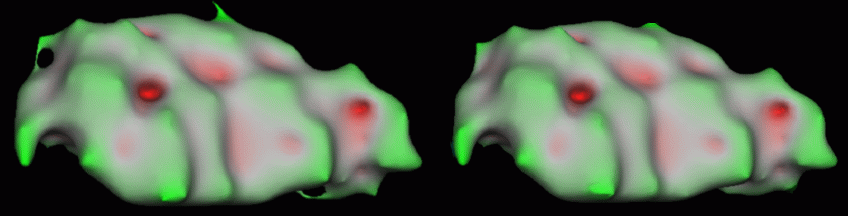
We present some results of the proposed method on subcortical segmentations and white matter segmentations. Topology correction of an individual structures takes a few seconds on a current machine. Most subcortical segmentations have few topological defects. Results show that addition and deletion of very few voxels is necessary to correct the topology of each structure. Manual segmentations are corrected by changing the labels of approximately 0.05% of the total number of voxels. Automatic segmentations requires of the order of 0.1% of labels to be changed. A typical example is given in the figure below, which shows the segmentation of the right pallidum before and after topology correction. The initial segmentation had 3 topological defects ( 3 handles: euler characteristic of the tessellation X = -4 ); the final surface has the correct spherical topology.
In order to validate the proposed algorithm, we have apply our method to 25 brain segmentations, manually and automatically labeled. The Whole Brain Segmentation algorithm proposed by Fischl et al. in [5] was used to generate automatic brain segmentations and to generate the joint probabilities p(I(x),S(x)) for all voxels x. The pair of compatible digital connectivities that we use for all the experiences was (6,18).
We present some results of the proposed method on subcortical segmentations and white matter segmentations. Topology correction of an individual structures takes a few seconds on a current machine. Most subcortical segmentations have few topological defects. Results show that addition and deletion of very few voxels is necessary to correct the topology of each structure. Manual segmentations are corrected by changing the labels of approximately 0.05% of the total number of voxels. Automatic segmentations requires of the order of 0.1% of labels to be changed. A typical example is given in the figure below, which shows the segmentation of the right pallidum before and after topology correction. The initial segmentation had 3 topological defects ( 3 handles: euler characteristic of the tessellation X = -4 ); the final surface has the correct spherical topology.
Correction of the topology of the cortical surface
is a much more challenging task: its highly convoluted nature often causes
numerous topological defects, which interact with each other, and are
difficult to precisely locate and correct. We have applied our method
to 25 brains in order to generate white matter segmentations with a correct
spherical topology. Before applying
the algorithm, we merge the ventricles into the white matter segmentation in order to avoid topological defects to be introduced in this area. We note that the following medical structures: caudate, putamen and pallidum nucleus, are considered to be part of the white matter segmentation. We apply the algorithm on each hemisphere separately. A binary segmentation S o of an hemisphere white matter contains on the order of 10 5 voxels (100 3 image domain). Similarly to subcortical segmentation results, approximately 0.1% of the total number of white matter voxels (approximately 100 voxels) need to have their label changed to achieve topology correction.
the algorithm, we merge the ventricles into the white matter segmentation in order to avoid topological defects to be introduced in this area. We note that the following medical structures: caudate, putamen and pallidum nucleus, are considered to be part of the white matter segmentation. We apply the algorithm on each hemisphere separately. A binary segmentation S o of an hemisphere white matter contains on the order of 10 5 voxels (100 3 image domain). Similarly to subcortical segmentation results, approximately 0.1% of the total number of white matter voxels (approximately 100 voxels) need to have their label changed to achieve topology correction.
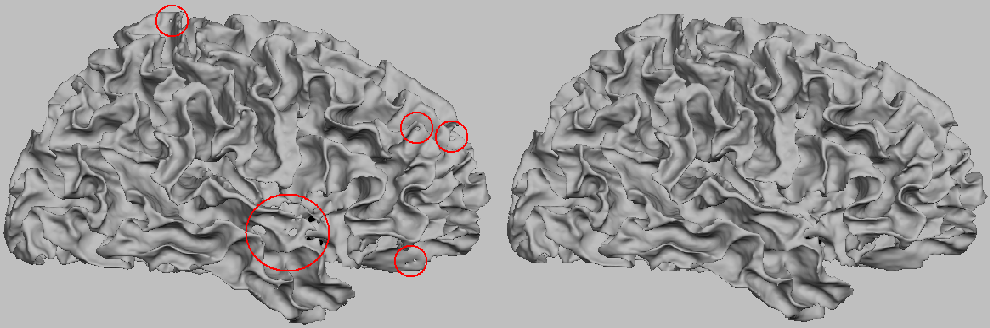
Initial Surface and Final Surface. The initial surface, generated under (n,n) = (6,18), has an
euler characteristic of X = -236. Some topological defects are circled in red.
Main References:
[1] X. Han, C. Xu,
D. Tosun, and J. L. Prince, "Cortical Surface Reconstruction Using
a Topology Preserving Geometric Deformable Model,'' MMBIA, Kauai, Hawaii,
Dec. 2001, pp. 213-220.
[2] G. Bertrand, ``Simple Points, topological numbers and geodesic meighborhood in cubid grids,'' Pattern Recognition Letters, vol. 15, pp. 1003-1011, 1994.
[3] X. Han, C. Xu, U. Braga-Neto, and J. L. Prince, "Topology correction in brain cortex segmentation using a multiscale, graph-based approach," IEEE Trans. Med. Imag., vol. 21(2): 109--121, 2002.
[4] N. Kriegeskorte and R. Goeble, ``An efficient algorithm for topologically segmentation of the cortical sheet in anatomical mr volumes. NeuroImage, vol. 14, pp. 329-346, 2001.
[5] B. Fischl et al. ``Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain''. Neuron, vol. 33,pp. 341-355, 2002.
[2] G. Bertrand, ``Simple Points, topological numbers and geodesic meighborhood in cubid grids,'' Pattern Recognition Letters, vol. 15, pp. 1003-1011, 1994.
[3] X. Han, C. Xu, U. Braga-Neto, and J. L. Prince, "Topology correction in brain cortex segmentation using a multiscale, graph-based approach," IEEE Trans. Med. Imag., vol. 21(2): 109--121, 2002.
[4] N. Kriegeskorte and R. Goeble, ``An efficient algorithm for topologically segmentation of the cortical sheet in anatomical mr volumes. NeuroImage, vol. 14, pp. 329-346, 2001.
[5] B. Fischl et al. ``Whole Brain Segmentation: Automated Labeling of Neuroanatomical Structures in the Human Brain''. Neuron, vol. 33,pp. 341-355, 2002.
Publications:
F. Ségonne, E. Grimson, and B. Fischl. "Topological Correction of Subcortical Segmentation", MICCAI 2003, LNCS 2879, Part 2, pp. 695-702.
F. Ségonne, E. Grimson, and B. Fischl, "Topological Correction of Digital Images," AI Memo, in progress.
F. Ségonne, E. Grimson, and B. Fischl. "Topological Correction of Subcortical Segmentation", MICCAI 2003, LNCS 2879, Part 2, pp. 695-702.
F. Ségonne, E. Grimson, and B. Fischl, "Topological Correction of Digital Images," AI Memo, in progress.