A Hybrid Approach
to the Skull Stripping Problem in MRI
F.Ségonne *° A.M. Dale *°
E.Busa ° M.Glessner ° D.Salat
° H.K.Hahn ¤ B.Fischl *°
* MIT A.I. Lab, ° Athinoula A. Martinos Center
- MGH / NMR Center, ¤ Mevis Bremen
Abstract: We present a novel skull-stripping algorithm based
on a hybrid approach that combines watershed algorithms and deformable
surface models. Our method takes advantage of the simplicity and
robustness of the former, while using the accuracy and surface information
available to the latter. The algorithm first localizes a single
white matter voxel in a T1-weighted MRI image, and uses it to create
a global minimum in the white matter before applying a watershed algorithm
with a pre-flooding height. The watershed algorithm builds an initial
estimate of the brain volume based on the three dimensional connectivity
of the white matter. This first step is simple and robust, and performs
well in the presence of intensity non-uniformities and noise, but
may erode parts of the cortex that abut bright non-brain structures such
as the eye sockets, or may remove parts of the cerebellum. In order to
correct these inaccuracies, a surface deformation process fits a smooth
surface to the masked volume, allowing the incorporation of geometric constraints
into the skull-stripping procedure. A statistical atlas, generated
from a set of accurately segmented brains, is used to verify the segmentation,
eventually corrects it, and the MRI intensity values are locally re-estimated
at the boundary of the brain. Finally a high-resolution surface deformation
is performed that accurately matches the outer boundary of the
brain, resulting in a robust and automated procedure. We successfully
segmented hundreds of data sets, acquired using a variety of scanners
and pulse sequences, without adjusting any parameters. The final surfaces
accurately fit the pial surface of the cortex, often removing thin,
sheet-like, non-brain tissues.
Methods:
Regarding brain antomy, our approach relies on a few general
assumptions:
- Similar to other approaches, our first basic assumption is
the connectivity of the white matter. The white matter (WM) constitutes
a connected region that is bordered by gray matter ( GM) and
cerebrospinal fluid (CSF). In T1-weighted M.R.Images, WM
voxels have bright intensities and are surrounded by darker A
hybrid approach to the skull stripping problem in MRIGM voxels
and even darker CSF voxels.
- The brain surface, which separates brain from non-brain regions,
is a smooth manifold with relatively low curvatue. In addition, we note
that these surfaces have similar global shapes, which motivates the use
of statistical atlas to ensure that an extracted brain volume possesses
the shape of a brain within a certain tolerance.
Deformable surface models are attractive techniques in that
they permit the incorporation of geometric and atlas-based information
into a deformation process targeting the brain surface. However, these
methods often reuiqre a good initialization, positioning the initial
active contour close enough to the final targeted surface in order to
avoid local minima. On the other hand, some recent watershed methods
have proven robustness to noise and could lead to a good initial extraction
of the brain surface. For this reason, we have decided to combine an initial
watershed brain extractoin with a subsequent deformable surface model.
Thus, the skull-stripping consists of a series of sequential
steps. First, some relevant parameters are estimated from the input image.
Next, a watershed algorithm is performed on the intensity image, with
a global minimum initialized within the cerebral white matter. Finally,
a deformable surface procedure is applied to the output of the
watershed algorithm to recover parts of the cortex that may have been
erroneously removed, using smoothness constraints on the shape of the
skull and atlas information.
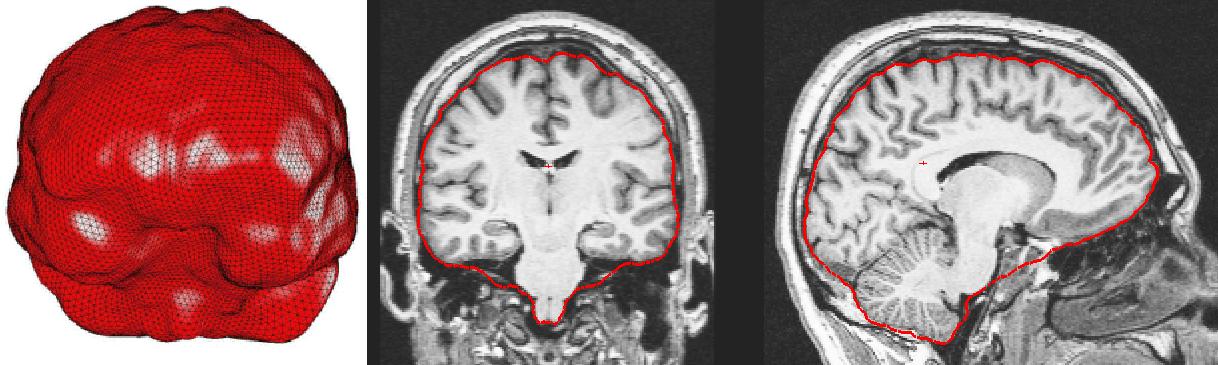
The following movies illustrate the watershed segmentation.
A brain volume is iteratively extracted from the original image and
most of the non-brain tissue are excluded. The basic assumption of
the watershed algorithm is the connectivity of the white matter
. This step performs well in the presence of intensity non-uniformities
and noise.
|
|
|
|
|
|
coronal section
|
horizontal section
|
sagital section
|
3D rendering
|
Next, the initial brain surface is iteratively refined using
global statistics. The template is deformed during a few iterations
in order to prevent large deviations due to the presence of non-uniformities.
Once the model has been 'accurately' matched onto the initial brain volume,
the shape of the brain is assessed and corrected if necessary by comparing
it to an average brain shape compiled from successfully segmented brains.
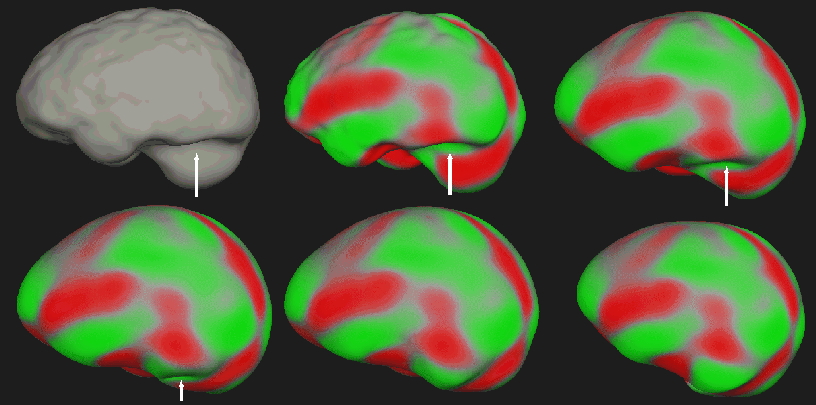
The following image shows the correction of the brain shape when part of
the cerebellum was excluded by the watershed algorithm.
Finally, the brain surface is matched onto the pial surface using
local estimates of brain parameters, such as the GM and CSF
intensities and variances.
Results and Conclusion :
Stripping the skull and other non-brain tissues from the structural
images of the head is a challenging and critical component for a variety
of post-processing tasks. Large anatomical variability among brains,
different acquisition methods, and the presence of artifacts increase
the difficulty of designing a robust algorithm, thus current techniques
are often susceptible to problems and require manual intervetion. in order
to validate the proposed algorithm, we compared it to 4 existing techniques,
and suggest ways of characterizing the correctness of the segmentation.
We compared our algorithm to four other existing automated skull-stripping
programs: the FMRIB's Brain Extraction TOOL (BET v1.2), FreeSurfer's
Stipp Skull (denoted FSS), Hahn and Peitgen's watershed algorithm (denoted
WAT), and Brain Surface Extractor (BSE). We refer to our method as HWA.
In order to assess the validity of each segmentation, we ran a study
on 43 T1-weighted brain volumes that had also been manually skull
stripped. Hence, we were able to use the manually segmented brain images
as a gold standard for comparison. The results of the validation study
can be found in the corresponding publication (Neuroimage, Vol 22/3 pp
1060-1075). Click on the following image to see some skull stripping results.
Our approach, based on a hybrid approach, which combines watershed
algorithms and deformable surface models, offers the user both the robustness
of watershed algorithms and the accuracy of deformable surface models.
Surface-based methods, which easily incorporate geometric information,
do not have access to interior intensity information, whereas watershed
methods ignore geometric information. Our Hybrid method, combining both
approaches, achiebes better results than either one individually. In our
experince, the proposed algorithm is robust to noise, artifacts and bias
fields. Other groupd studies have shown that our method outperformed several
others, proved to be more sensitive and robust, and most successfully
retained brain tissue even within the difficult AD group.
This skull stripping technique is part of the cortical surface
reconstruction and flatenning software FreeSurfer.
Publications :
F. Ségonne, A.M. Dale, E. Busa, M. Glessner, D. Salat,
H. K. Hahn, and B. Fischl, "A hybrid approach to the skull stripping
problem in MRI," Neuroimage, Vol 22/3 pp 1060-1075.
F. Ségonne: "Unsupervised Skull Stripping in MRI", Masters
Thesis, co-supervised by O. Faugeras and B. Fischl, MIT AI Lab, June
2002 .