
System: (Polymer gel network + solvent inside) inside the control volume (c.v.)., i.e., the control volume is changing as the get network is expanding due to absorbing the surrounding solvent fluid.
Additional Modeling Assumptions:
The Donnan membrane equilibrium phenomena is due to the balance between the diffusion tendencies and the electrical attraction/repulsion among ions/fixed charge groups. Since the equilibrium condition require the ions in both regions to have equal potential while also requiring to satisfy the electroneutrality condition, the electric potential develop across the gel/membrane interface. It should be noted that the macroscopic electroneutrality is valid for dimensions much greater than the Debye length.
Consider the ionic gel immersed in ionic solvent bath as shown above. Assuming the concentration of the mobile ions in both the gel and the solvent bath are much smaller that the concentration of polymer or solvent, the mobile ion concentration can be considered as dilute, and the electrochemical potential of the ions can be described by
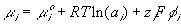
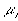 is the electrochemical potential of the ion,
is the electrochemical potential of the ion,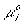 is the chemical potential of the pure ion species,
is the chemical potential of the pure ion species,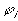 is the electrical potential of the ion.
is the electrical potential of the ion.
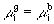
where
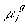 is the electrochemical potential of the ion inside the gel, and
is the electrochemical potential of the ion inside the gel, and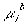 is the electrochemical potential of the ion in the solvent bath.
is the electrochemical potential of the ion in the solvent bath.
or, since 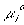 is the same for the g and b phases, we have
is the same for the g and b phases, we have
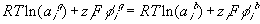
or
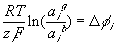
where
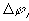 is
is 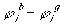 ,
the electrical potential difference across the gel-bath interface. Since this
electrical potential difference is common to all ions, the activity coefficient
ratio across the interface of different ions, say i and j, can be
related as
,
the electrical potential difference across the gel-bath interface. Since this
electrical potential difference is common to all ions, the activity coefficient
ratio across the interface of different ions, say i and j, can be
related as
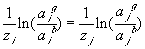
For the 1:1 electrolyte where zi = 1 and zj = -1, the above expression reduces to
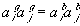
For the case where the activity coefficients in the g- and b-phases are equal or for the ideal dilute solution case, we can also write
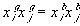
or

The electroneutrality conditions of both the bath and the gel are
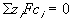 for external bath
for external bath
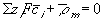 for inside the gel/membrane
for inside the gel/membrane
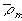 is the fixed charge group density, and
is the fixed charge group density, and
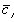 is the ion concentration inside the gel/membrane.
is the ion concentration inside the gel/membrane.
The Donnan equilibrium and electroneutrality conditions, along with charge conservation relations, can be used to compute individual ion concentrations. Stictly speaking, the above result applies to true equilibrium case. However, in general, it can also be applied to non-equilibrium case as long as the net transport is much slower than the diffusion or the drift components of the transport process.
The transport of ions due to diffusion and migration in the electrolytic medium is described by widely used relation (neglecting the connective contribution)
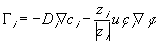
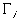 is the molar flux of the ith species ion,
is the molar flux of the ith species ion,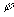 is the electrical potential.
is the electrical potential.Assuming both the concentration and electrical potential gradient inside the gel near its interface is linear and considering only one dimensional case for simplification, then the average ion transport into the gel at the interface can be written as
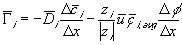
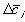 ,
,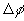 is the
ion concentration and electrical potential differences between inside
the gel near its interface and outside bath, i.e.
is the
ion concentration and electrical potential differences between inside
the gel near its interface and outside bath, i.e.
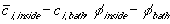 ,
and
,
and 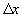 is the distance in between. The first term describes the diffusion component
due to the concentration gradient, and the second term describes the migration
component due to the electric potential gradient. Since the electric potential
gradient is commonly experienced by all ions, it is the source of coupling
effect among ions. Studying the expression for the ion transport above, one
can easily represent this using the bond graph structure
is the distance in between. The first term describes the diffusion component
due to the concentration gradient, and the second term describes the migration
component due to the electric potential gradient. Since the electric potential
gradient is commonly experienced by all ions, it is the source of coupling
effect among ions. Studying the expression for the ion transport above, one
can easily represent this using the bond graph structure
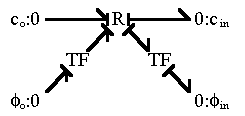
The ions with greater diffusivity will tend to move across the medium at faster rate than the ions with lower diffusivity. However, such tendency for charge separation induces local electric field among ions, and it in turn acts to retard the faster ions and to accelerate the slower ions. For instance, if the faster ions are positively charged whereas the slower ions are negatively charged, then positive local electric potential gradient will build up to retard the positive ions and to accelerate the negative ions. Such "local" electric field, which acts in the scale of a few Debye length, is quite large and it is rather difficult to induce charge separation in macroscopic scale. Therefore, in macroscopic scale, the electroneutrality prevails.
The electrical potential coupling among ions can be modeled as a simple ideal parallel plate capacitor (Oster)
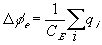
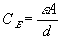
where
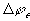 is the induced electric potential,
is the induced electric potential,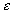 is the dielectric constant of the electrolyte,
is the dielectric constant of the electrolyte,The bond graph representation is simply
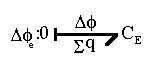
Note that the induced electric potential 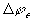 here only models the aporoximate effect of bulk electroneutrality in uniform
medium, and therefore it does not model the electric potential difference
between two regions of different medium.
here only models the aporoximate effect of bulk electroneutrality in uniform
medium, and therefore it does not model the electric potential difference
between two regions of different medium.
In addition to the macroscopic electroneutrality coupling among ions in each region of uniform electrolytic medium (bulk electroneutrality), there also exists electric potential gradient between two regions of unequal ion concentrations. For example, the Donnan equilibrium membrane potential is the electric potential difference across the membrane induced by the balance between the individual ion diffusion tendencies and the bulk electroneutrality in each region. In order to describe the electric potential profile exactly, one needs to solve the Gauss' law which relates the electric field gradient to the net charge at a point
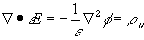
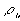 is the net charge (in fact, the electroneutrality effect in previous section
may also be solved using Gauss' law directly). However, not only the analysis
is non-trivial and computation intensive, the exact electric potential profile
is not of concern for our purpose. Therefore, we will model the electric
potential difference between two uniform media region as the average of the
individual ion specie's contribution at near equilibrium (quasistatic)
condition. Defining the reference electrical potential to be at the
surrounding bath when it is electrically neutral, the individual ion
contribution and the average electric potential at a region are modelled as
is the net charge (in fact, the electroneutrality effect in previous section
may also be solved using Gauss' law directly). However, not only the analysis
is non-trivial and computation intensive, the exact electric potential profile
is not of concern for our purpose. Therefore, we will model the electric
potential difference between two uniform media region as the average of the
individual ion specie's contribution at near equilibrium (quasistatic)
condition. Defining the reference electrical potential to be at the
surrounding bath when it is electrically neutral, the individual ion
contribution and the average electric potential at a region are modelled as
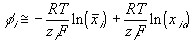
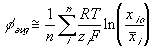
The total electric potential at a region then may be expressed as
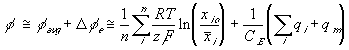
Applying this expression to the surrounding bath, we get
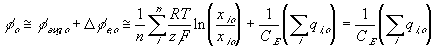
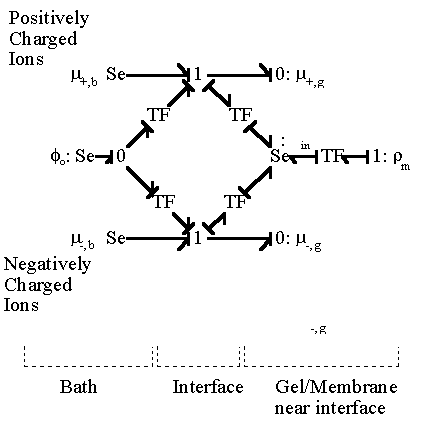
and the electrical potential of surrounding bath becomes zero, i.e. reference potential, when it is electrically neutral as defined previously. The bond graph representation of the ion transport across two region based on the above results is

Applying the above bond graph structures to the case of 1:1 electrolyte transport at the gel/membrane interface, we then have
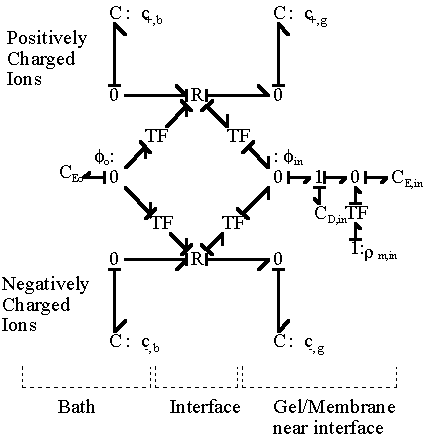
In most cases, the external solvent bath may be modelled as the ideal ions/solvent source as well as the electric potential reference ground where the bulk electroneutrality is always satisfied, in which case the bond graph representation then simpliflies to
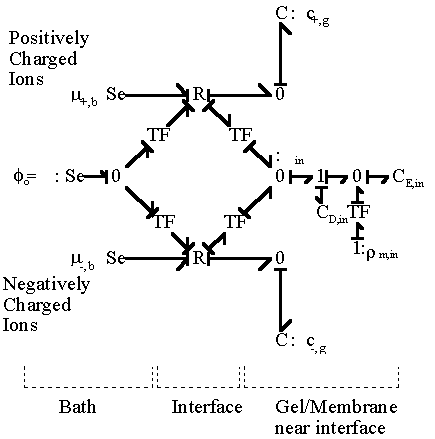
Chemical Capacitances:
With the assumption of dilute solution, the chemical potential of ion in the gel may be described by
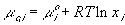
Treating the polymer molecule as solvent/ion size molecule with equivalent scaling factor, x, the effective mole fraction of ion, xi is then
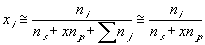
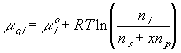
Safely assuming the solvent concentration changes at much slower rate than the individual ion concentration, the rate of change of ion's chemical potential may be approximated by
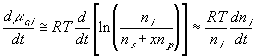
Electrical Capacitances:
As mentioned previously, the capacitance field describing the Donnan potential and the electroneutrality with respect to surrounding bath as the reference potential is expressed as
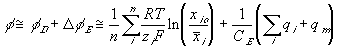
or
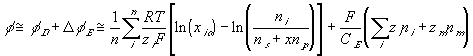
The rate of change of electric potential is then
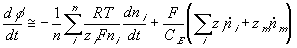
The ion transport kinetics of the resistive element is simply
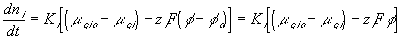
Comparing this expression to the generally used ion transport equation
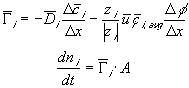
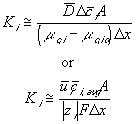
For our model, we will use the average value of the above Ki's.
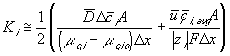
The resulting system equations for the case of 1:1 binary electrolyte are then
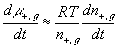
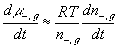
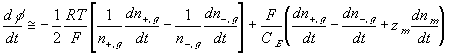
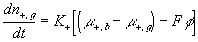
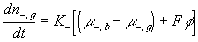
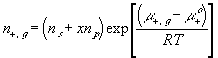
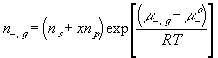
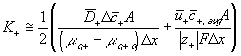
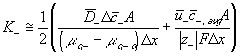
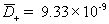 ,
diffusivity of plus (H+) ion [m2/sec]
,
diffusivity of plus (H+) ion [m2/sec]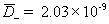 ,
diffusivity of negative (Cl-) ion [m2/sec]
,
diffusivity of negative (Cl-) ion [m2/sec]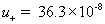 ,
mobility of plus (H+) ion [m2/(volt*sec)]
,
mobility of plus (H+) ion [m2/(volt*sec)]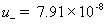 ,
mobility of negative (Cl-) ion [m2/(volt*sec)]
,
mobility of negative (Cl-) ion [m2/(volt*sec)]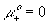 ,
standard chemical potential of pure plus ion, H+
,
standard chemical potential of pure plus ion, H+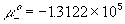 ,
standard chemical potential of pure negative ion, Cl-
,
standard chemical potential of pure negative ion, Cl-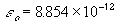 ,
dielectric contant of vaccum [coul2/(N*m2)]
,
dielectric contant of vaccum [coul2/(N*m2)]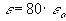 ,
dielectric constant of the electrolyte
,
dielectric constant of the electrolyte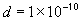 ,
typical maximum separation of charges; a few Debye length [m]
,
typical maximum separation of charges; a few Debye length [m]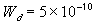 ,
Donnan interface width [m]
,
Donnan interface width [m]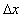 =
Wd/2, approximate separation between bath and interface unit [m]
=
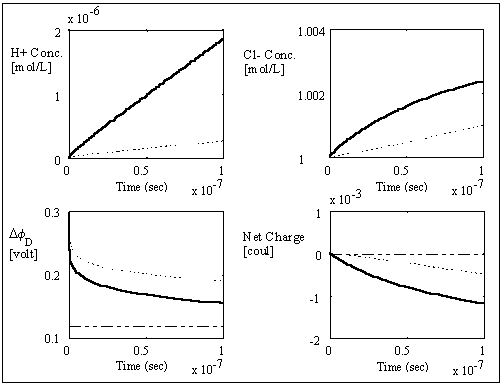
Wd/2, approximate separation between bath and interface unit [m]For the purpose of testing the ion transport model at the gel/membrane interface, the change in solvent concentration of the control volume is not included. In addition, the diffusivities and mobilities of H+ and Cl- ions in the gel control volume is assumed to be in the same order of magnitude as in the aqueous solution. Note that both the diffusivity and the mobility of H+ ion is much greater than of Cl- ion. In general, this implies much faster transport of H+ than of Cl- in neutral medium. However, in a highly positively charged medium, the H+ will be electrically repelled from the medium, and the Cl- concentration in the gel is thus expected to be much higher than H+'s. Therefore, one can expect the K+ to be much smaller than the K- since the average concentration of the H+ will be much smaller than the Cl- at the interface.
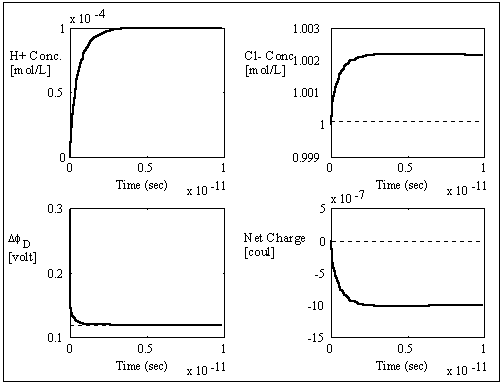
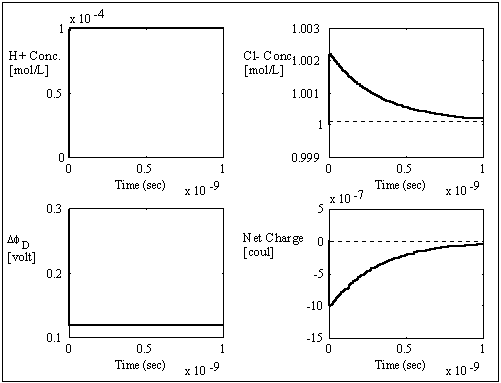
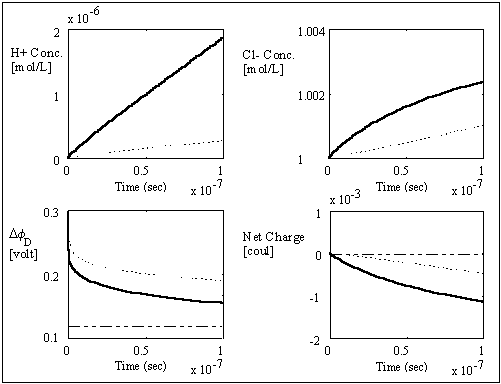
The computer simulation results based on these assumptions and above
parameters are shown in the above figures with two different time scales. The
dashed lines are the theoretically expected equilibrium values whereas the
solid lines are the simulation result values. As expected, the average
transport coefficient of Cl- obtained from the simulation was much greater than
of H+ with values 7.05x10-3
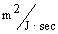 and 3.23x10-4
and 3.23x10-4
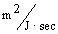 respectively, resulting in overshoot of Cl- concentration before settling to
equilibrium value. The situation is reversed for the case of negatively charged
gel/membrane system, i.e. zm = -1, as shown in the computer simulation
results below.
respectively, resulting in overshoot of Cl- concentration before settling to
equilibrium value. The situation is reversed for the case of negatively charged
gel/membrane system, i.e. zm = -1, as shown in the computer simulation
results below.
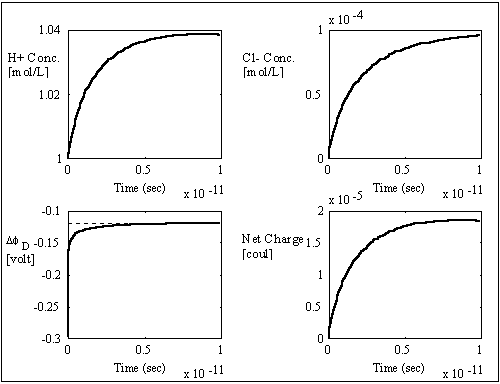
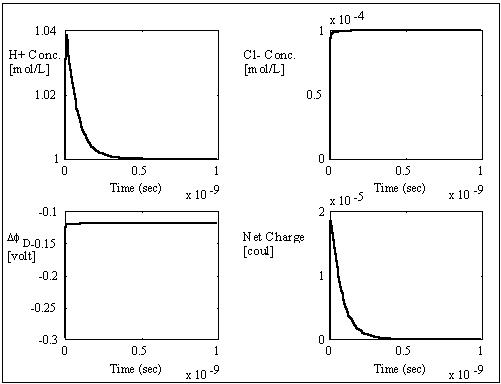
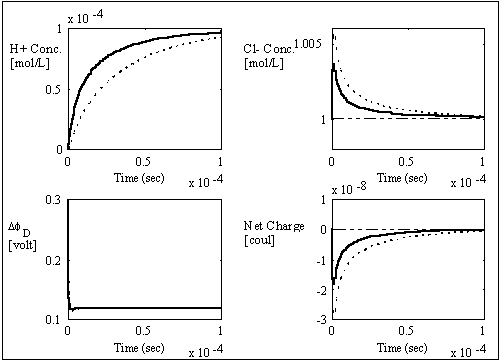
The simulation values converged to the expected values very well, and the overall ion transport process took roughly 1x10-11 seconds which is many magnitudes smaller than the typical response time of the gel/membrane. Therefore, this simulation result justifies the assumption of quasi-equilibrium between the surrounding bath and the region near the interface (assuming the typical gel/membrane are thicker than the Debye length by several orders of magnitude). For such quasi-equilibrium case with fixed charge density, the above system equations then reduces to the Donnan equilibrium condition and the bulk electroneutrality at the interface region.
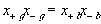
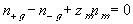
It should be noted that the transport rate of establishing Donnan equilibrium condition is extremely fast due to large local electric field coupling among ions/fixed charged groups within the Debye length of the solvent bath/gel interface. Therefore, in most case, the Donnan equilibrium condition and the bulk electroneutrality is valid even in the non-equilibrium case with net transport, and they may be employed as the boundary conditions for the states of gel/membrane's bulk units. In such cases, the combined effect of Donnan equilibrium condition and bulk electroneutrality can be treated as effort (electric potential) source, and the bond graph representation further reduces to
The electric potential source term on the right hand side exerts the necessary electric potential on the ions based on the concentrations of the both positive and negative ions and membrane fixed charges to achieve both the Donnan equilibrium condition and bulk electroneutrality, i.e., combining the bulk electroneutrality and Donnan equilibrium condition yields the mole fractions and the electric potential of the ions
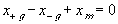
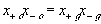
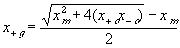
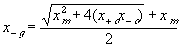
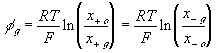
The bulk of the gel/membrane model is identical to the gel/membrane interface model discussed in previous section. It is assumed to be quasistatic with uniform state properties such as ion/solvent concentrations, fixed charge density, and temperature, and as with the interface, the strong electric field coupling among ions and fixed charged prevails inducing macroscopic bulk electroneutrality at equilibrium
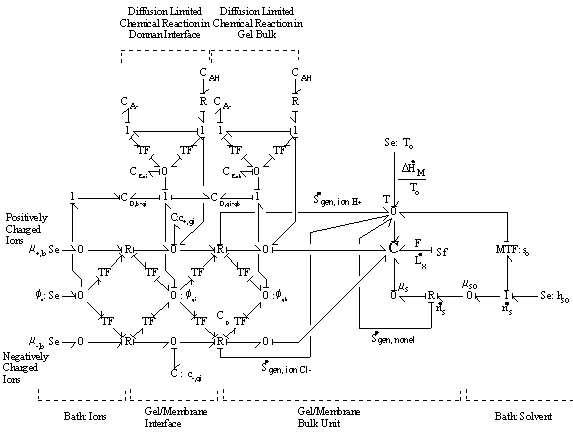
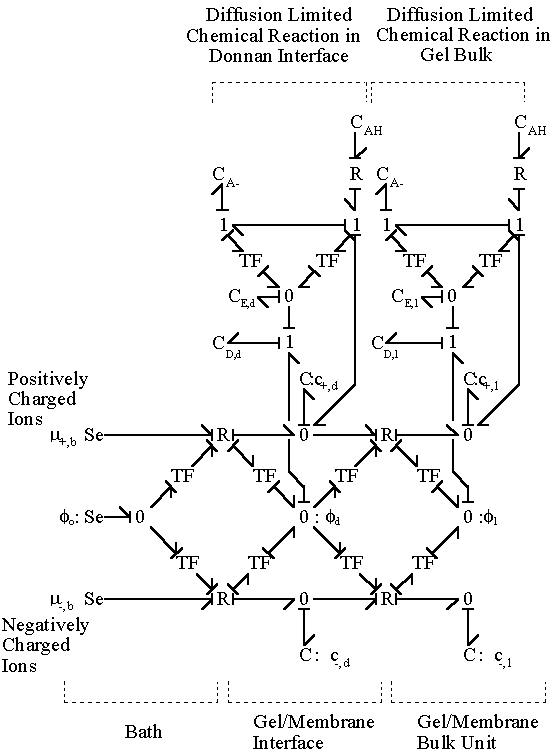
The bond graph structure of the gel/membrane interface and two gel/membrane bulk units connected in series is
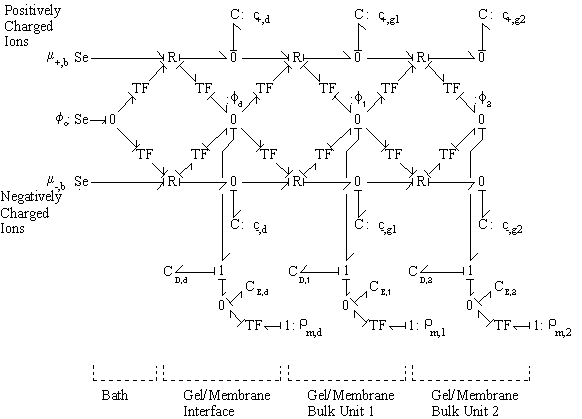
According to above bond graph model, the electric potential differences can exist even among the bulk units during the transport process since the internal pH and subsequently the fixed charge density of each unit may well differ from others. This electric potential differences would vanish at equilibrium though when the uniform fixed charge density is achieved among interface/bulk units. The governing equations of each bulk unit are identical to the ones for the interface unit. The governing dynamic equations for the above system of the interface unit connected to two bulk units in series are
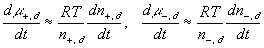
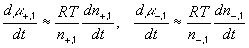
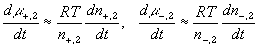
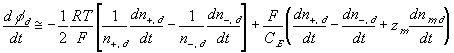
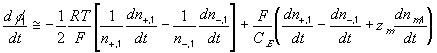
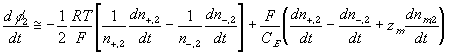 where
where
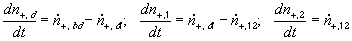
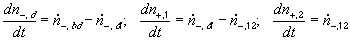
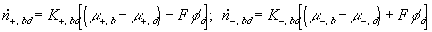
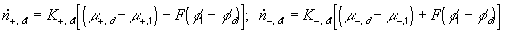
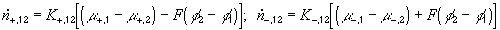
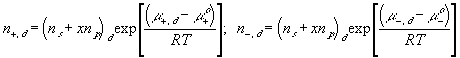
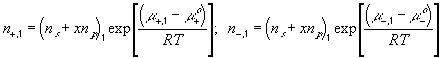
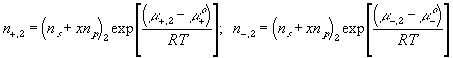
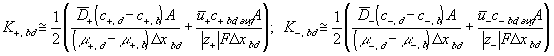
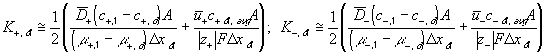
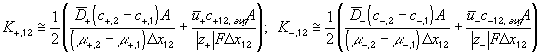
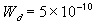 , width of the interface unit [m]
, width of the interface unit [m]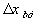 = Wd/2, approximate separation between bath and the interface unit [m]
= Wd/2, approximate separation between bath and the interface unit [m]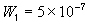 , width of the bulk unit 1 [m]
, width of the bulk unit 1 [m] = W1/2, approximate separation between the interface unit and the bulk
unit 1 [m]
= W1/2, approximate separation between the interface unit and the bulk
unit 1 [m] , width of the bulk unit 2 [m]
, width of the bulk unit 2 [m] = W1/2 + W2/2, approximate separation between the bulk unit 1 and the
bulk unit 2 [m]
= W1/2 + W2/2, approximate separation between the bulk unit 1 and the
bulk unit 2 [m]
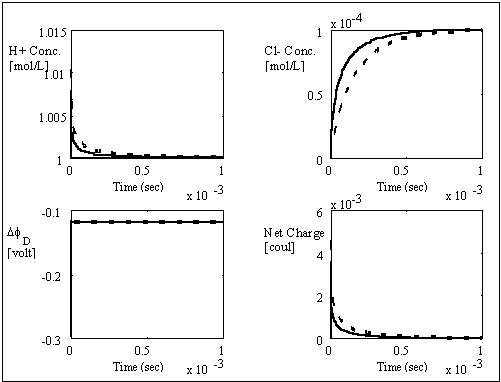
As expected, the interface unit's much faster kinetic has negligible influence on the bulk units' behaviors, and the results are almost identical to the results of the initial model which incorporates the interface unit dynamics. The simplified model is further simulated to t = 1x10-4 seconds where the states converge to the equilibrium values well as shown below.
Similarly, the computer simulation results for the case of negatively charged gel/membrane system are shown below.
As the ion moves into the gel/membrane network, it may also react with the fixed charged side groups. Namely diffusing H+ or OH- in solvent can react with corresponding conjugate basic or acidic structures on the network, and it was shown that such diffusion-reaction can significantly slow down the overall ion transport process (Grodzinsky). As the ions are moving into the gel/membrane network while reacting with the fixed charges of network simultaneously, not only the overall kinetic of the ion's transport is affected, also the concentrations of both the mobile ions and the fixed charge groups are changed as well, subsequently changing the overall equilibrium behavior. Therefore, proper integration of the dynamic model of ion diffusion/reaction process is necessary.
Assuming the predominant chemical reaction is the acid/base reaction between the H+/OH- and the fixed charge groups, we will limit the discussion to acid/base reaction only. However, the results can easily be translated to other types of reactions as well.
Let's consider the case of gel/membrane with negatively charged fixed side groups. For the side groups with the pKa below 7, the side group is positively charged when the internal pH is above the pKa, whereas the side group is neutral when the internal pH is below the pKa. When the pH is equal to the pKa, this implies exactly half of the total side group is dissociated. In acidic environment, there are two reactions occuring simultaneously. First, the neutral side group of gel/membrane network can dissociate into the anion and the hydronium ion
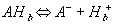
where
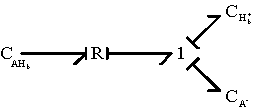
The chemical reaction is represented by a two-port resistance field, and the thermal (entropy generation) port is not included. In the case where the thermal port is of importance, it can be modified as
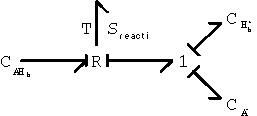
Second, the hydrogen ion diffusing in from outside can associate with the network-bound anion, A- to form the neutral side group.
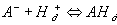
where
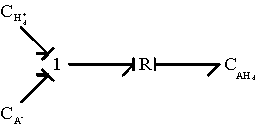
Combining the above two reactions, we have
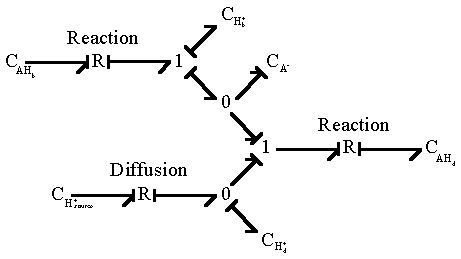
Since Hd+ is identical to Hb+, the overall bond graph representation of diffusion/reaction simplies to
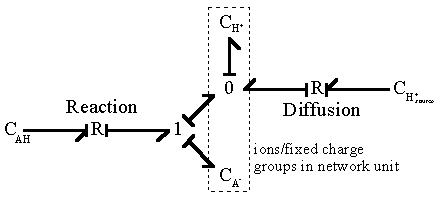
UL>
According to the simple mass-action law for elementary chemical reaction such as
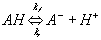
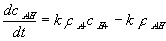
where the equilibrium constant Keq in this case would then be
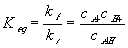
For simplicity, let's model both the fixed sidegroups and the hydrogen ions as dilute solutions, i.e.,
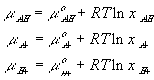
where xAH, xA- and xH+ are mole fractions of -AH, -A- and H+ respectively. Since concentrations of -AH, -A- and H+ are much smaller than the concentration of solvent, the mole fractions can be related to corresponding concentrations as
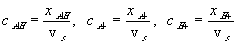
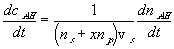
The reaction kinetic expression can then be expressed as
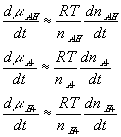
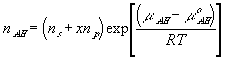
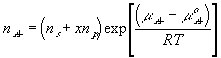
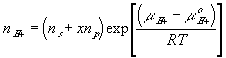
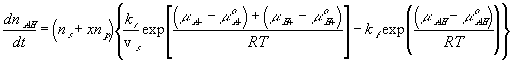
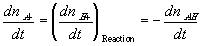
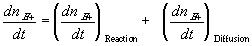
In many cases, simplifications can be made with assumption that the reaction occurs at much faster rate than the diffusion, and thus can be considered as "instantaneous" and "always" at equilibrium (quasi-equilibrium). This does not imply that the concentrations of -A-, H+ or -AH do not vary with time, but they change at a rate much slower than the reaction rate, limited by the diffusion of the hydrogen ion into the gel/membrane unit. The quasi-equilibrium reaction model says at every instant of time
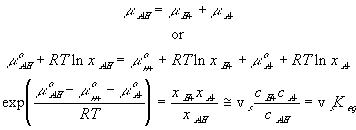
Since the total possible number of the binding site -A is fixed
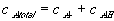
the equilibrium constant Keq can also be written as
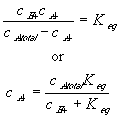
Differentiating this with respect to time, we get
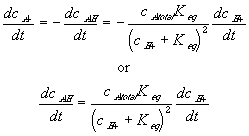
For such quasi-equilibrium reaction, the bond graph representation of the diffusion-reaction then reduces to
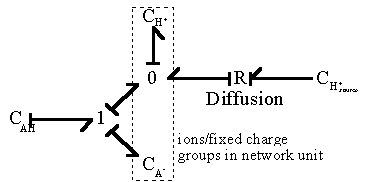
Note that the bond graph model shows only two out of total three capacitances have integral causality implying only two capacitances are independent energy storage elements whereas the other one is dependent. This result is in agreement with the above analysis since the -AH and -A- concentrations are dependent of each other. As with the Donnan quasi-equilibrium model considered previously, the dissipated energy (heat of reaction) and the entropy generation are assumed to be unimportant in the overall dynamics of the ion's transport for the quasi-equlibrium chemical reaction model.
Combining the models of the gel/membrane's Donnan interface and the bulk with the diffusion limited chemical reaction described above for the case of binary solution (H+, Cl-), we arrive at the following model. The chloride ion is a completely dissociated ion of the strong acid, HCl, and is assumed not to react or bind with other ions or fixed charges. The dissociation of gel bound groups -AH produces fixed charges -A- and hydronium ion H+ which in turn influences the ion transport in the gel through changing both the H+ concentration and the electric potential. The electric field coupling, however, does not affect the dissociation chemistry of -AH since the valences of produced charges are exactly opposite (i.e. +1 for H+ and -1 for -A-) and therefore their electrical effects cancel each other out exactly. For the complete model of polyelectrolyte gel, following model needs to be incorporated into the model describing the swelling behavior of the gel.
Similarly to the nonelectrolyte gel model, the quasistatic differential energy change of the control volume due to the mixing/diffusion within the gel itself can be expressed as
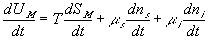
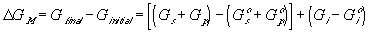
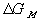 for the nonelectrolyte gel.
for the nonelectrolyte gel.
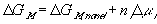
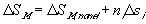
or
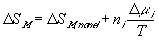
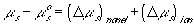
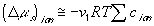 (van't Hoff equation)
(van't Hoff equation)
The bond graph representation of the polyelectrolyte gel's mixing process derived above can be expressed as
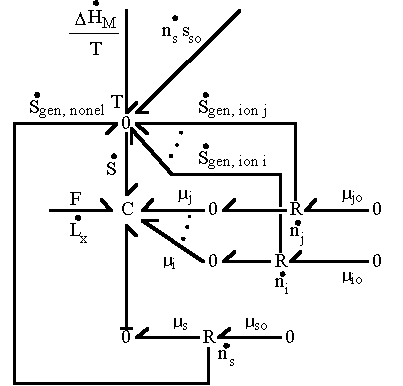
Combining the above results for the binary mobile ion specie case, we have