MASSACHUSETTS INSTITUTE OF TECHNOLOGY
ARTIFICIAL INTELLIGENCE LABORATORY
A.I.Memo No. 1331
November, 1991
Dynamic Model and Control of an Artificial Muscle based on Contractile Polymers
David L. Brock
Abstract
A dynamic model and control system of an artificial muscle is presented.
The artificial muscle is based on a contractile polymer gel which undergoes
abrupt volume changes in response to variations in external conditions.
The device uses an acid-base reaction to directly convert chemical to
mechanical energy. A nonlinear sliding mode control system is proposed to
track desired joint trajectories of a single link controlled by two
antagonist muscles. Both the model and controller were implemented and
produced acceptable tracking performance at 2Hz.
1 Introduction
In 1950 W. Kuhn and A. Katchalsky produced a fiber which contracts in
response to changes in pH (Kuhn 1950). In their demonstration a
single fiber immersed in a fluid repeated raised and lowered a weight
proportional to the hydrogen ion content of the solvent. It was
proposed at the time that such a device could be used as a linear
actuator. One of the major drawbacks however was the exceeding slow
response time, on the order of minutes. Since then a number of
innovations have made this artificial ``muscle'' worthy of further
study. First, fibers have been produced which contract in seconds and
even tenths of seconds (DeRossi 1987; Suzuki 1989). Second, some
fibers support considerable loads, on the order of 100N/ (DeRossi 1988). The
contraction rates and forces have become comparable, and in some cases
even exceeding, that of a human muscle. Third, the physics of fiber
contraction (or gels as they are more generally called) have become
well understood (Tanaka 1973a - 87b). Finally, technological
innovations such as robotics and implantable artificial biological
organs have created a demand for such devices. A number of
contractile gel devices have already been constructed, such as a robot
gripper (Caldwell 1990), a multifingered hand (Toyota 1990), and an
artificial urethral sphincter (Chiarelli 1988; DeRossi 1985; 86).
(DeRossi 1988). The
contraction rates and forces have become comparable, and in some cases
even exceeding, that of a human muscle. Third, the physics of fiber
contraction (or gels as they are more generally called) have become
well understood (Tanaka 1973a - 87b). Finally, technological
innovations such as robotics and implantable artificial biological
organs have created a demand for such devices. A number of
contractile gel devices have already been constructed, such as a robot
gripper (Caldwell 1990), a multifingered hand (Toyota 1990), and an
artificial urethral sphincter (Chiarelli 1988; DeRossi 1985; 86).
The design of these devices from a practical engineering perspective,
particularly with regard to dynamic modeling and control has only been
considered recently (Genuini 1990).
In this paper we will
consider the design of a simple linear actuator based on contractile
gel fibers as well as the design and simulation of single mechanical
linkage controlled by two antagonist muscles. The first section will
discuss the design of a simple linear actuator and the second will
present a dynamic model along with approximate parameter
estimates. The third section will introduce a nonlinear sliding mode
controller which achieves desired trajectory tracking for model
inputs.

Figure 1-1.
Two antagonist artificial muscles
control a single link.
2 Design
Although there are many possible actuator designs, this paper
will focus on the direct chemical to mechanical energy
conversion through the control of the hydrogen ion content in the muscle
fibers. The basic concept is to use high performance miniature
valves to the control the inflow of acid or base
to modulate pH and control contraction.
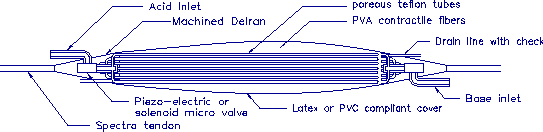
A schematic diagram of the proposed actuator is shown in figure 2-1.
Two input lines containing 0.1M HCL and 0.1M NaOH enter the muscle at
the base. A miniature value placed into the base material controls
the inflow of fluid. An irrigation system design to facilitate mixing is
composed of numerous small tubes which are interspersed among the fibers.
Finally, a drainage tube allows the waste fluid (i.e. salt water) to be removed.
The tubes and wetting surfaces of the valves are constructed from teflon
which is chemically inert and the fibers are made from Poly-Vinyl Alcohol
PVA. Although many different contractile materials exist
(Tanaka 1990), PVA has been used successfully by a number of researchers and
has a relatively high tensile strength. The tendons are made of Spectra
and the tendon to PVA connections are machined Delran. The fibers are affixed
at their terminations with epoxy which is also chemically inert.
3 Model
The dynamic model of the system is composed of three basic parts:
the fluid conveyance system, the hydrogel contractile fibers and
the mechanical linkage. The following sections will address each of
these systems in detail.
3.1 Fluid System
A schematic diagram of the fluid system is shown in figure 3-1. It is
assumed the inlet fluid line is under a moderate pressure 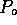 and a microvalve with controllable
resistance
and a microvalve with controllable
resistance 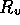 modulates the
inflow of fluid. The system of irrigation lines is modeled as a fluid
resistance
modulates the
inflow of fluid. The system of irrigation lines is modeled as a fluid
resistance 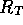 and an inertance
I. Finally, the compliant sheath into which the fluid flows is
modeled as a capacitance C and the exit line, a resistance
and an inertance
I. Finally, the compliant sheath into which the fluid flows is
modeled as a capacitance C and the exit line, a resistance 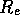 .
.
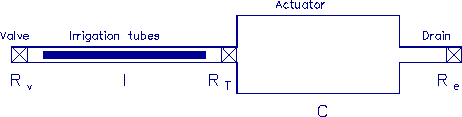 Figure 3-1. The fluid model consists of a pressure source
P_o at the inlet of the system. The valve, tubes and drain line
are modeled as fluid resistances R_v, R_T and R_e respectively.
Finally, a fluid inertance I is included to account for the mass of
the fluid and a capacitance C to model the expansion of the actuator
chamber.
Figure 3-1. The fluid model consists of a pressure source
P_o at the inlet of the system. The valve, tubes and drain line
are modeled as fluid resistances R_v, R_T and R_e respectively.
Finally, a fluid inertance I is included to account for the mass of
the fluid and a capacitance C to model the expansion of the actuator
chamber.
Valve
Although there are commercially available metering valves which
continuously modulate flow, they are generally too large from this
application. Commercial piezo-electric or solenoid fluid values also
exist in the appropriate size, although they have only two states,
open and closed. It may be possible to use binary state valves in
a pulse width modulation scheme to meter fluid, but this may
introduce undesirable affects such as water hammer,
excessive part wear and slower response. Alternatively there
are some experimental metering valves and pumps which are of the
correct dimension (in fact some are significantly smaller than this
application demands creating the possibility of very small linear
actuators). It may also be possible to use molecular valves in the form
of biological or artificial membranes whose porosity is controlled
by small voltages.
In any case it is assume some mechanical valve of the appropriate
dimension can be constructed, either a commercial two-state valve or
an experimental multi-state valve. Based on commercial data sheets
for fluid resistance we can approximate the resistance of a valve by

where 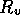 is fluid resistance in N
is fluid resistance in N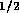 sm
sm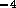 ,
,
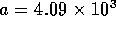 N
N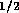 sm
sm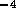 ,
, 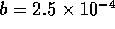 m/v, and
m/v, and 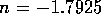 are constants. For two-state valves we will assume
are constants. For two-state valves we will assume
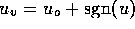 and for multi-state valves
and for multi-state valves
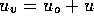 , where
, where 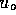 is some small value and u is the
control signal input, 0 to 12 v. These parameters where roughly based
on values given for the LEE Interface Fluidic 2-way (normally closed)
microvalve. This valve is energized with 12 v at 250mW, switches in
1.5 msec and operates in a 0 to 7 psi pressure range. The relation of
pressure to flow is given by
is some small value and u is the
control signal input, 0 to 12 v. These parameters where roughly based
on values given for the LEE Interface Fluidic 2-way (normally closed)
microvalve. This valve is energized with 12 v at 250mW, switches in
1.5 msec and operates in a 0 to 7 psi pressure range. The relation of
pressure to flow is given by

where 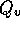 is
flow rate in m
is
flow rate in m /s,
/s, 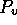 is pressure in N/m
is pressure in N/m and
and 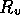 is fluid resistance N
is fluid resistance N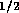 sm
sm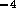 .
.
Irrigation System
Multiple porous tubes attempt to
uniformly enter and mix the fluid to increase the response time of the
actuator. Consider a single tube as shown in figure 3-2. The tube has
an inner radius 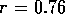 mm and a
straight length l = 10 cm after a 90
mm and a
straight length l = 10 cm after a 90 elbow of radius
elbow of radius 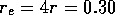 cm. Small holes of radius
cm. Small holes of radius 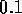 mm are punctured in the teflon tubes. The holes are
small enough so that an initial pressure
mm are punctured in the teflon tubes. The holes are
small enough so that an initial pressure 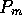 is necessary to induce flow. This prevents back flow
into the acid-base lines, but for this initial model we will assume
is necessary to induce flow. This prevents back flow
into the acid-base lines, but for this initial model we will assume
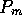 is zero. The holes are place
at 90
is zero. The holes are place
at 90 intervals about the
cross section and every 1 mm along the length.
intervals about the
cross section and every 1 mm along the length.
Suppose the tube
as we describe is non-porous and open at the end. If we assume a
fully developed flow under an entrance pressure of 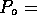 1 kPa (above atmospheric), the fluid flow is
1 kPa (above atmospheric), the fluid flow is

where 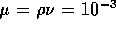 kg/m s (for water, 25
kg/m s (for water, 25 C ),
C ),
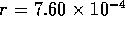 m, and l = 0.1 m.
This yields a flow of
m, and l = 0.1 m.
This yields a flow of 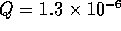 m
m /s and an average fluid velocity
of
/s and an average fluid velocity
of 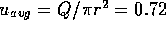 m/s. The Reynolds number
is Re
m/s. The Reynolds number
is Re 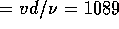 , where
, where 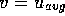 ,
, 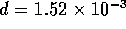 m and
m and 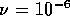 m
m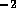 /s, which is below the critical
value Re
/s, which is below the critical
value Re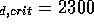 ; therefore we may
assume the flow is laminar. For higher pressures, equation
1 yields Reynolds numbers in the
turbulent range, but the significant resistance offered by the sealed
porous tube reduce the flow rates and maintains laminar conditions. As
we will later show the maximum flow rate is approximately
; therefore we may
assume the flow is laminar. For higher pressures, equation
1 yields Reynolds numbers in the
turbulent range, but the significant resistance offered by the sealed
porous tube reduce the flow rates and maintains laminar conditions. As
we will later show the maximum flow rate is approximately 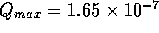 m
m /s, which yields
/s, which yields 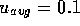 m/s and
m/s and 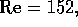 which is certainly laminar. Finally, the entrance region before the
fully developed flow is approximately
which is certainly laminar. Finally, the entrance region before the
fully developed flow is approximately  Re
Re  cm;
therefore we can assume the boundary layer is fully develop within the
entire length of the tube.
cm;
therefore we can assume the boundary layer is fully develop within the
entire length of the tube.
The wall shear force will result in a
head loss and thereby create non-uniformity flows through the small
irrigation holes. However, since the flow will decrease along the
length due to seepage, the head loss will not be linear as in the case
of homogeneous circular tubes. To approximate the head loss we will
assume continuous porosity and a uniform fully developed flow at each
point x of tube. The wall shear stress is given by

which results in a pressure
gradient
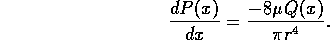
If we assume
a flow loss due to porosity
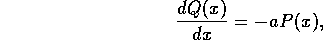
we have the resulting differential equation

where 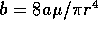 . If we solve this differential
equation with boundary conditions
. If we solve this differential
equation with boundary conditions 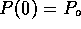 and
and 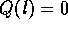 , we
have the head loss as a function of length
, we
have the head loss as a function of length
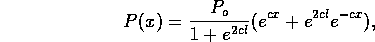
where 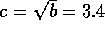 m
m . The head loss in the tube
is not significant in this case as shown in figure 3-2.
. The head loss in the tube
is not significant in this case as shown in figure 3-2.
 Figure 3-2. Head loss due to wall shear force in the circular
porous tube can generally be ignored.
Figure 3-2. Head loss due to wall shear force in the circular
porous tube can generally be ignored.
For the purposes of the dynamic model, it may be more more useful to
represent the entire porous tube system as a fluid resistance 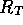 . Following a simplified
convention, we will assume the fluid resistance is given by
. Following a simplified
convention, we will assume the fluid resistance is given by

where R is fluid
resistance 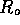 is the resistance
due to the entrance,
is the resistance
due to the entrance, 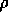 is the
resistance per unit length and l is the length of the tube.
The entrance resistance is given by
is the
resistance per unit length and l is the length of the tube.
The entrance resistance is given by

where d is the inner diameter of the tube in meters, 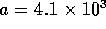 and
and 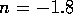 . For the tubes
. For the tubes 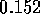 cm in diameter
cm in diameter 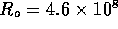 N
N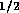 sm
sm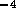 . The resistance per unit length
. The resistance per unit length

where 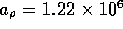 N
N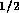 sm
sm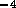 ,
, 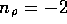 , and d is the inner
diameter. For the tube described above, the resistance per unit
length is
, and d is the inner
diameter. For the tube described above, the resistance per unit
length is 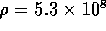 N
N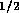 sm
sm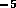 ,
thus the total resistance for the tube is
,
thus the total resistance for the tube is 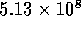 N
N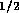 sm
sm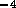 . Using equation 2 to compute the resistance of the
irrigation holes, we have a resistance
. Using equation 2 to compute the resistance of the
irrigation holes, we have a resistance 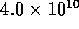 N
N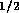 sm
sm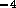 for holes
for holes 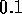 mm in diameter. However with 80 holes/cm and
10 cm of tube, the total resistance is
mm in diameter. However with 80 holes/cm and
10 cm of tube, the total resistance is 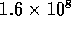 N
N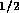 sm
sm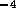 .
.
For the acid and base
systems we will have six irrigation tubes each, resulting in a total
fluid resistance of 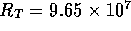 N
N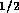 sm
sm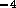 The relation between pressure and flow is again given
by,
The relation between pressure and flow is again given
by,

Inertance
Although the inertance of the fluid is small,
fast switching times may cause its effects to be important. The
inertance is given by

where 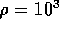 kg/m
kg/m is the fluid density,
is the fluid density, 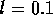 m is the length of the tubes and
m is the length of the tubes and 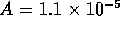 m
m is the total cross sectional area. For this system,
the fluid inertance is
is the total cross sectional area. For this system,
the fluid inertance is 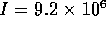 kg/m
kg/m and
the dynamics are given by
and
the dynamics are given by

Suppose the fluid accelerates to 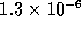 m
m /s in 10 ms under a pressure of 1 kPa. Then the
inertance I would be
/s in 10 ms under a pressure of 1 kPa. Then the
inertance I would be 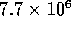 kg/m
kg/m . This is comparable to
the value given for the model. So for switching times on the order of
1 ms, inertance effects become significant.
. This is comparable to
the value given for the model. So for switching times on the order of
1 ms, inertance effects become significant.
Capacitance
In this particular design, the fiber system is covered with a
compliant sheath. Since it is flexible, it can be approximated as a
fluid capacitance; that is, when fluid is forced into the chamber the
sheath will stretch and resist the flow. If we model the sheath as a
thin-walled uniform cylinder with closed ends, the elemental stress
tensor is given by 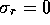 ,
, 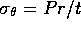 ,
, 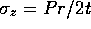 and
and 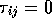 ,
where P is the pressure, t is the wall thickness and
r is the radius. Given the generalized stress-strain relations,
,
where P is the pressure, t is the wall thickness and
r is the radius. Given the generalized stress-strain relations,

and the
strain-displacement equations

we can solve for the change in volume as a
function of pressure
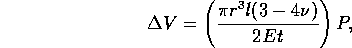
where E is the Elastic Modulus and  is Poisson's ratio. Therefore the fluid capacitance
is
is Poisson's ratio. Therefore the fluid capacitance
is
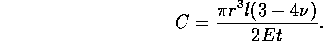
If r = 1
cm, l = 10 cm, 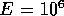 N/m
N/m (approximate for
rubber),
(approximate for
rubber), 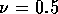 and
and 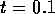 mm,
mm,
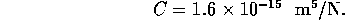
With a fluid flow of 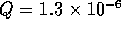 m
m /s, this
capacitance will become significant if the pressure changes more than
1 MPa in a 1 ms. Therefore we will ignore the capacitance.
/s, this
capacitance will become significant if the pressure changes more than
1 MPa in a 1 ms. Therefore we will ignore the capacitance.
Drain
The drain line consists of a single tube 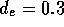 cm and a check valve. Employing
equation 2, this results in a
fluid resistance of
cm and a check valve. Employing
equation 2, this results in a
fluid resistance of 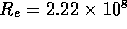 N
N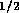 sm
sm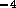 , for a drain line 20 cm in length.
, for a drain line 20 cm in length.
Fluid
dynamic equations
The elemental pressures are related by
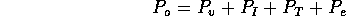
and the flows by
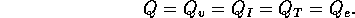
Substituting the
elemental relations, we have
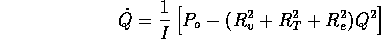
where Q is the flow into the fibers. Note
the steady state flow rate for the open valve is
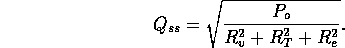
For a fully open value 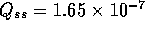 m
m /s. Note the total volume of injected fluid is
/s. Note the total volume of injected fluid is

Mixing and
Diffusion
When the fluid (either acid or base) is
injected into the fiber network there is a certain lag time before the
entire system uniformly equilibrates to the new concentration. We
could model this mixing as the diffusion of HCl or NaOH in water. If
the tubes are uniformly spaced as in figure 3-3, we can draw
concentric circles around each with radius 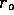 equal to half the distance between the tubes. The
mixing time could be approximated, as the time for the fibers at
radius
equal to half the distance between the tubes. The
mixing time could be approximated, as the time for the fibers at
radius 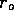 to experience a
certain concentration of fluid. As a simplification we can
approximate the diffusion with the one dimension diffusion equations
to experience a
certain concentration of fluid. As a simplification we can
approximate the diffusion with the one dimension diffusion equations

where J is the
diffusion flux per unit area, c is the concentration in moles
per volume and D is a constant. The solution is the standard
diffusion model
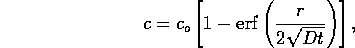
where
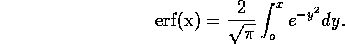
The boundary
concentration 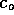 , of course,
decreases as particles diffuse into the liquid. However, as a first
order approximation to the diffusion time, we assume
, of course,
decreases as particles diffuse into the liquid. However, as a first
order approximation to the diffusion time, we assume 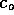 is constant. Then the concentration at
is constant. Then the concentration at 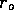 is one-half its initial value
when
is one-half its initial value
when 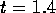 ms for
ms for 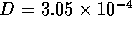 m
m /s (0.1M HCL at 25
/s (0.1M HCL at 25 C ) and
C ) and 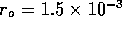 m.
m.
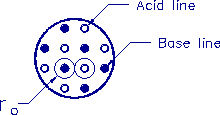 Figure 3-3. Arrangement of acid and base lines in the cross
section of the muscle.
Figure 3-3. Arrangement of acid and base lines in the cross
section of the muscle.
The diffusion model, however, is highly inaccurate since the exit
velocity from the pores in the teflon tubes is relatively high and
together with the motion of the fibers will cause turbulent mixing,
not diffusion. Therefore as a simple approximation, we will assume the
fluid mixing and diffusion is a first order lag, hence

where c is the concentration of acid or base in the solvent,
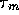 is a time constant which we
will take to be
is a time constant which we
will take to be 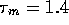 ms (based
roughly on the previous discussion) and
ms (based
roughly on the previous discussion) and 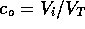 ratio of solute to solvent, where
ratio of solute to solvent, where 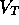 is the total volume of the actuator,
is the total volume of the actuator, 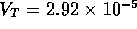 m
m .
.
3.2 Contractile Fibers
pH
The contractile fibers respond roughly linearly to pH, so it is
important to calculate the pH in the solution based on the amount
of acid or base entered into the chamber.
An acid is a chemical species having the tendency to lose a proton
and a base is a species tending to accept a proton. The quantitative
measure of acid strength is the acid dissociation constant; that is the
equilibrium constant for the reaction
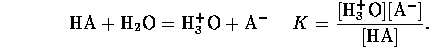
Along with this reaction there is always the self dissociation of water

If the original amount of acid A added to the solution is
[HA]o, then the material balance relation is given by
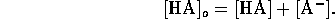
Also the solution must be electrically neutral, hence
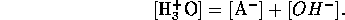
Solving these equations for the hydrogen ion concentration yields the
cubic
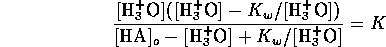
However, we may assume that the 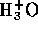 from water is negligible
compared to that from the acid, hence
from water is negligible
compared to that from the acid, hence 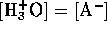 . We may
assume that for strong acids there is complete dissociation; that is
. We may
assume that for strong acids there is complete dissociation; that is
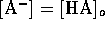 , which yields the trivial result
, which yields the trivial result

Similarly, for base a B we have equilibrium
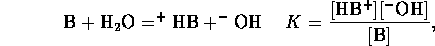
mass balance,

and electric neutrality
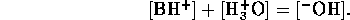
Now we can assume total dissociation

which is a valid except for very high concentrations. Also we
can assume the contribution of  from self-ionization of water is
negligible, hence
from self-ionization of water is
negligible, hence
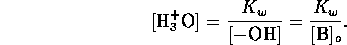
Considering the strong acid and base together we can assume
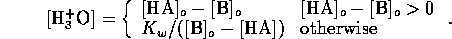
Since pH is 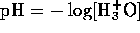 , we have
, we have
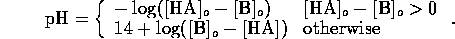
Diffusion
Besides the lag due to mixing among the fibers, there is a lag
due to the diffusion within the fibers themselves. This lag is
due to bulk macromolecular rearrangement of the polymers in the
network and is approximately proportional to the square of the
cross sectional diameter. The time constant is

where d is the diameter in meters and 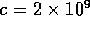 s/m
s/m .
Thus for fibers 10
.
Thus for fibers 10 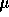 m in diameter contract in approximately 0.1 s.
This can also be approximated to the first order by
m in diameter contract in approximately 0.1 s.
This can also be approximated to the first order by

where 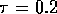 , pH is the pH in the fiber
and pHs is that in the
solvent. Notice this time constant is substantially slower than the one
given in equation 3. Therefore we will ignore the lag due
to mixing and consider only the diffusion within the fiber as the major
delay.
, pH is the pH in the fiber
and pHs is that in the
solvent. Notice this time constant is substantially slower than the one
given in equation 3. Therefore we will ignore the lag due
to mixing and consider only the diffusion within the fiber as the major
delay.
Hydrogel Physics
A gel is a cross-linked network of polymers immersed in a fluid,
which can undergo a volume phase transition in response to changes in external
conditions such as temperature, solvent, pH, light and electric fields.
Three competing forces act on the polymer gel network: rubber elasticity,
polymer-polymer affinity and hydrogen ion pressure. Competition between
these forces, collectively called the osmotic pressure, determine
the equilibrium volume of the network. The phase transition has been
analyzed in terms of the mean field theory of swelling equilibrium of gels.
The osmotic pressure of a gel is given by Flory's equation,
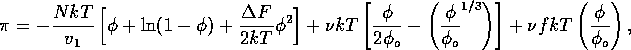
where N is Avogadro's number, k is the Boltzmann constant,
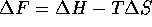 represents the difference
between the free energies of a polymer segment-segment
and polymer-solvent interaction, and
represents the difference
between the free energies of a polymer segment-segment
and polymer-solvent interaction, and
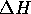 and
and 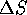 are the enthalpy and entropy respectively.
In equilibrium, the osmotic pressure is zero.
Thus by solving the above equation, we can theoretically
compute the fiber force. However because of its complexity and
because of the availability of empirical data, we can describe the
contraction of the fiber with the simple model shown in figure 3-4.
The intrinsic force per unit area is
are the enthalpy and entropy respectively.
In equilibrium, the osmotic pressure is zero.
Thus by solving the above equation, we can theoretically
compute the fiber force. However because of its complexity and
because of the availability of empirical data, we can describe the
contraction of the fiber with the simple model shown in figure 3-4.
The intrinsic force per unit area is 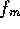 is approximately
is approximately
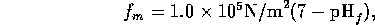
assuming a total cross sectional area 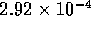 m
m ,
the intrinsic force is
,
the intrinsic force is 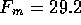 N(7-pH
N(7-pH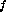 ).
Also the intrinsic stiffness is
).
Also the intrinsic stiffness is
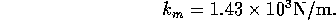
and viscous damping is roughly estimated as

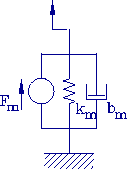 Figure 3-4. Simple model of contractile fiber.
Figure 3-4. Simple model of contractile fiber.
3.3 Mechanical System
A model of the mechanical system is shown in figure 3-5. Assuming linear
components for this part of the model, we have
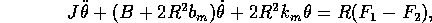
where

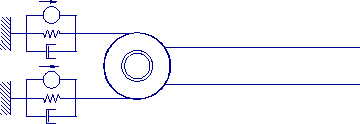 Figure 3-5. Single link controlled by two antagonist muscles.
Figure 3-5. Single link controlled by two antagonist muscles.
3.4 Summary
Using the model as outlined above we have the following system equations
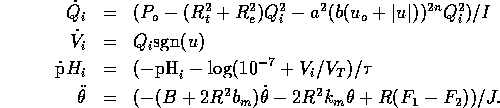
However before we design a controller for this system let us consider a number of
simplifications. First, the lag due to the inertance of the fluid is negligible
compared with the dynamics of the rest of the system. This was verified in a full
dynamic simulation of the system, although it is fairly obvious since the time
constant of the fluid flow is on the order of 10 ms while the diffusion lag is
about 100 ms. This assumption allows us to compute the flow Q directly from the
input u. Thus we can reduce the order of the system by two and take the
input to be the flow rate 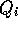 . In order simplify this problem further let us
assume a single-input single-output system, by taking the co-contraction
of the actuators as an offset force and controlling position through feedback
through a single actuator. With these initial assumptions let us write the system
equations in the form
. In order simplify this problem further let us
assume a single-input single-output system, by taking the co-contraction
of the actuators as an offset force and controlling position through feedback
through a single actuator. With these initial assumptions let us write the system
equations in the form

Specifically,

where

and
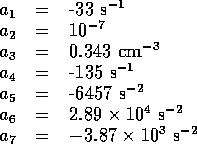
4 Control
We wish to control the joint angle 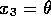 using the simplified model
presented above. We would also like the controller to
maintain zero tracking error in the presence of modeling errors. Therefore,
we will design a non-linear sliding mode controller.
using the simplified model
presented above. We would also like the controller to
maintain zero tracking error in the presence of modeling errors. Therefore,
we will design a non-linear sliding mode controller.
However before we attempt a construct a controller
for this fourth order system, let us initial consider one further simplification.
Based on the numerical estimates of the model parameters the damping ratio of
the linear mechanical dynamics is 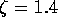 . Therefore let us initially
assume the inertia can be neglected, and produce a controller based on the
reduce third order system,
. Therefore let us initially
assume the inertia can be neglected, and produce a controller based on the
reduce third order system,
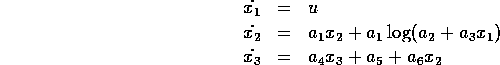
where

and
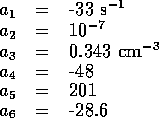 <
<
Now the controllability canonical form,
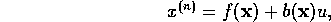
where 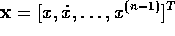 ,
can be derived by differentiating the equation for the joint
angle three times.
,
can be derived by differentiating the equation for the joint
angle three times.
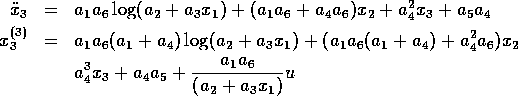
Let 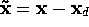 be the tracking error on
be the tracking error on 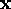 and
define the sliding surface to be
and
define the sliding surface to be
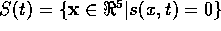 , where
, where
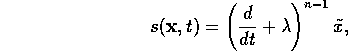
for some positive 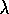 . Hence
. Hence

Thus maintaining zero tracking error is equivalent to the first-order stabilization
problem in s. In addition a bound on s implies a bound on the tracking error
vector; that is if 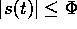 , then
, then
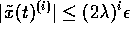 . We must now design a controller
such that for all
. We must now design a controller
such that for all 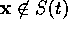 ,
,
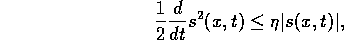
for some positive 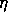 .
The estimation of f is given by
.
The estimation of f is given by 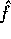 and the bounds on the error is
and the bounds on the error is

Similarly, the term b is estimated by
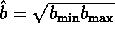 where
where 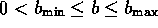 . If we let
. If we let
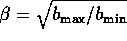 , then
, then

and the control law
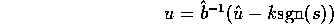
for s given above,
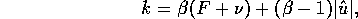
and
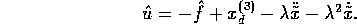
In this case we chose 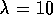 s
s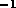 to be approximately equal to the natural
frequency of the system while the estimate errors to be approximately 10% the nominal values.
to be approximately equal to the natural
frequency of the system while the estimate errors to be approximately 10% the nominal values.
5 Simulation
In order to get a sense of the model dynamics a 1Hz sinusoidal input was given to the system.
A plot of the pH as a function of time is shown in figure 5-1 and the joint angle
in figure 5-2. The sliding mode controller discussed in the previous section was implemented
and simulated for a desired joint trajectory
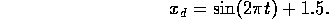
Figure 5-3 shows the pH and figure 5-4 shows the desired and actual joint position. Notice
desired tracking is achieved after approximately 0.5 seconds. Figure 5-5 shows the effect
of neglected link inertia. Note the joint trajectory is offset by approximately 10 Fourth and fifth order sliding mode controllers were attempted to compensate for the link
inertia and fluid inertance, but were found to be numerically unstable in the calculation
of the higher order derivatives. Numerical filters corrected this problem, though the
simulation times became unacceptable long. A more judicious choice of numerical parameters
could possibly correct this problem.
Fourth and fifth order sliding mode controllers were attempted to compensate for the link
inertia and fluid inertance, but were found to be numerically unstable in the calculation
of the higher order derivatives. Numerical filters corrected this problem, though the
simulation times became unacceptable long. A more judicious choice of numerical parameters
could possibly correct this problem.
 Figure 5-1. pH in the polymer fibers in response to a 1Hz input signal.
Figure 5-1. pH in the polymer fibers in response to a 1Hz input signal.
 Figure 5-2. Joint angle.
Figure 5-2. Joint angle.
 Figure 5-3. Response to pH to control joint trajectory.
Figure 5-3. Response to pH to control joint trajectory.
 Figure 5-4. Desired and actual (modeled) joint trajectories. Zero
tracking error is achieved after one second.
Figure 5-4. Desired and actual (modeled) joint trajectories. Zero
tracking error is achieved after one second.
6 Conclusion
A sliding mode controller produced reasonable tracking performance for input
sine waves on the order of 1-2 Hz, but deviated significantly at higher frequencies.
This seems reasonable based on the relatively long lag times introduced by the
polymer diffusion. It has been possible more recently, to produce even smaller
fibers (about 1 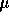 m), while using UV induced transectional cross-linking to
increase strength. These and other innovations should
allow faster response times for practical actuator development and controller
design.
m), while using UV induced transectional cross-linking to
increase strength. These and other innovations should
allow faster response times for practical actuator development and controller
design.
REFERENCES
in
- Chiarelli, P. and De Rossi, D., ``Determination of Mechanical Parameters
related to the Kinetics of Swelling in an Electrically Activated Contractile
Gel,'' Progress in Colloid and Polymer Science, Vol. 48, 1988.
- ---, et. al., ``Progress in the Design of an Artificial
Urethral Sphincter,'' Proc. of the 3rd Vienna International
Workshop on Functional Electrostimulation, Vienna Austria, Sept. 1989.
- ---, et. al., ``Dynamics of a Hydrogel Strip,''
In Press, Biorheology, 1990.
- ---, Umezawa, K, and De Rossi, D., ``A Polymer Composite showing
Electrocontractile Response,'' submitted to Journal of Polymer Science
Polymer Letters Edition
- De Rossi, D., et. al., ``Electrically Induced Contractile Phenomena in Charged
Polymer Networks Preliminary Study on the Feasibility of the Muscle-like Structures,''
Transactions of the American Society of Artificial Internal Organs XXXI,
p. 60-65, 1985.
- ---, et. al., ``Contractile Behavior of Electrically
Activated Mechanochemical Polymer Actuators,'' Transactions of the
American Society of Artificial Internal Organs XXXII, p. 157-162, 1986.
- --- and Chiarelli, P., ``Determination of Mechanical Parameters
related to the Kinetics of Swelling in an Electrochemically Actuated
Contractile Gel,'' Abstract 5th. International Seminar on Polymer
Physics, High Tatras, 1987.
- ---, et. al., ``Analogs of Biological Tissues for Mechanoelectrical
Transduction: Tactile Sensors and Muscle-Like Actuators,''
NATO ASI Series, Vol. F43, Sensors and Sensory Systems, 1988.
- Genuini, G., et. al., ``Psuedomuscular Linear Actuators: Modeling and
Simulation Experiences in the Motion of Articulated Chains,'' In Press,
NATO ACI Science, 1990.
- Itoh, Y., et. al., ``Contraction/Elongation Mechanism of Acrylonitrile Gel Fibers,''
Polymer Preprints - Japan (English Edition), Vol. 36, Nos. 5-10, p. E184, 1987.
- Katchalsky, A., et. al., Chapter ``Elementary Mechanochemical Processes,''
Size and Shape Changes of Contractile Polymers, Wassermann, A. ed.,
Pergamon Press, New York, 1960.
- ---, et. al., ``Reversible Dilatation and Contraction by Changing the State
of Ionization of High-polymer Networks,'' Nature, Vol. 165, p. 514-516.
- ---, Remel, A. and Walters, D. H., ``Conversion of Chemical into Mechanical
Energy by Homogeneous and Cross-striated Polymeric Systems,'' in Wassermann, A.,
(ed.), Size and Shape Changes of Contractile Polymers, Pergamon Press, New York,
p. 41-77, 1960.
- Kuhn, W., et. al., ``Reversible Dilatation and Contraction by Changing the State of
Ionization of High-polymer Acid Networks,'' Nature, Vol. 165, p. 514-516, 1950.
- --- and Tanaka, T., ``Study of the Universality Class of the Gel Network System,''
Journal of Chemical Physics, Vol. 90, No. 9, p.5161-5166, 1989.
- Morasso, P., et. al., ``Generation of Command Synergies for
Anthropomorphic Robots,'' Proc. IEEE of the Conference on Robotics and
Automation, 1990.
- Matsuo, Eriko Sato and Tanaka, Toyoichi, ``Kinetics of discontinuous volume-phase
transition of gels'', Journal of Chemical Physics, Vol. 89, No. 3, 1988.
- Nakatani, Y., Ourisson, G. and Tanaka, T., ``Osmotic Swelling of Phospholipid Vesicles,''
Biophysics Biochemical Research Communications, Vol. 110, p. 1320, 1983.
- Nicoli, D., et. al., ``Chemical Modification of Acrylamide Gels: Verification of
the Role of Ionization in Phase Transitions,'' Macromolecules, Vol. 16,
p. 887-891, 1983.
- Osada, T. and Hasebe, M., ``Electrically Actuated Mechanochemical Devices using
Polyelectrolyte Gels,'' Chemistry Letters,'', p. 1285-1288, 1985.
- Suzuki, M., et. al., ``An Artificial Muscle by Polyvinyl Alcohol Hydrogel Composites,''
Proc. of IUPAC-CHEMRAWN VI, Tokyo, 1987.
- Tanaka, T., Soda, K. and Wada, A., ``Dynamical Aspects of Helix-Coil Transitions in
Biopolymers I,'' Journal of Chemical Physics, Vol. 58, p. 5707, 1973.
- ---, Ishiwata, S and Ishimoto, C., ``Critical Behavior of Density Fluctuations
in Gels,'' Physical Review Letters, Vol. 38, p. 771, 1977.
- ---, ``Dynamics of Critical Concentration Fluctuations in Gels,''
Physics Review, V. A17, p. 763, 1978
- ---, ``Collapse of Gels and the Critical Endpoint,'' Physical Review Letters,
Vol. 40, p. 820, 1978.
- --- and Fillmore, D. J., ``Kinetics of Swelling of Gels,'' Journal of Chemical
Physics, Vol. 70, p. 1214, 1979.
- ---, ``Phase Transition in Gels and a Single Polymer,'' Polymer, Vol. 20, p. 1404,
1979.
- --- , et. al., ``Phase Transition in Ionic Gels,'' Physical Review Letters, Vol. 45,
p. 1636, 1980.
- --- , ``Gels'', Scientific American, p. 124-138, January 1981.
- --- , Nishio, I., Sun, S.T., and Ueno-Nishio, S., ``Collapse of Gels under
an Electric Field'', Science, Vol. 218, p. 467, 1982.
- ---, et. al., ``Mechanical instability of gels at the phase transition'',
Nature, Vol. 325, No. 6107, pp. 796-798, February 26, 1987.
- ---, ``Gels,'' in Structure and Dynamics of Biopolymers, edited by
Nicolini, C., Martinus Nijhoff Publishers, Boston, p. 237-257, 1987.
 (DeRossi 1988). The
contraction rates and forces have become comparable, and in some cases
even exceeding, that of a human muscle. Third, the physics of fiber
contraction (or gels as they are more generally called) have become
well understood (Tanaka 1973a - 87b). Finally, technological
innovations such as robotics and implantable artificial biological
organs have created a demand for such devices. A number of
contractile gel devices have already been constructed, such as a robot
gripper (Caldwell 1990), a multifingered hand (Toyota 1990), and an
artificial urethral sphincter (Chiarelli 1988; DeRossi 1985; 86).
(DeRossi 1988). The
contraction rates and forces have become comparable, and in some cases
even exceeding, that of a human muscle. Third, the physics of fiber
contraction (or gels as they are more generally called) have become
well understood (Tanaka 1973a - 87b). Finally, technological
innovations such as robotics and implantable artificial biological
organs have created a demand for such devices. A number of
contractile gel devices have already been constructed, such as a robot
gripper (Caldwell 1990), a multifingered hand (Toyota 1990), and an
artificial urethral sphincter (Chiarelli 1988; DeRossi 1985; 86). 

 and a microvalve with controllable
resistance
and a microvalve with controllable
resistance 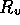 modulates the
inflow of fluid. The system of irrigation lines is modeled as a fluid
resistance
modulates the
inflow of fluid. The system of irrigation lines is modeled as a fluid
resistance 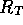 and an inertance
I. Finally, the compliant sheath into which the fluid flows is
modeled as a capacitance C and the exit line, a resistance
and an inertance
I. Finally, the compliant sheath into which the fluid flows is
modeled as a capacitance C and the exit line, a resistance 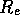 .
. 

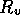 is fluid resistance in N
is fluid resistance in N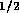 sm
sm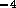 ,
,
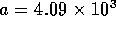 N
N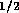 sm
sm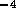 ,
, 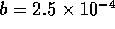 m/v, and
m/v, and 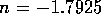 are constants. For two-state valves we will assume
are constants. For two-state valves we will assume
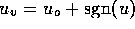 and for multi-state valves
and for multi-state valves
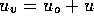 , where
, where 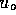 is some small value and u is the
control signal input, 0 to 12 v. These parameters where roughly based
on values given for the LEE Interface Fluidic 2-way (normally closed)
microvalve. This valve is energized with 12 v at 250mW, switches in
1.5 msec and operates in a 0 to 7 psi pressure range. The relation of
pressure to flow is given by
is some small value and u is the
control signal input, 0 to 12 v. These parameters where roughly based
on values given for the LEE Interface Fluidic 2-way (normally closed)
microvalve. This valve is energized with 12 v at 250mW, switches in
1.5 msec and operates in a 0 to 7 psi pressure range. The relation of
pressure to flow is given by 
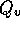 is
flow rate in m
is
flow rate in m /s,
/s, 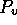 is pressure in N/m
is pressure in N/m and
and 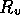 is fluid resistance N
is fluid resistance N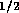 sm
sm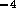 .
. 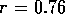 mm and a
straight length l = 10 cm after a 90
mm and a
straight length l = 10 cm after a 90 elbow of radius
elbow of radius 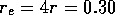 cm. Small holes of radius
cm. Small holes of radius 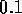 mm are punctured in the teflon tubes. The holes are
small enough so that an initial pressure
mm are punctured in the teflon tubes. The holes are
small enough so that an initial pressure 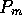 is necessary to induce flow. This prevents back flow
into the acid-base lines, but for this initial model we will assume
is necessary to induce flow. This prevents back flow
into the acid-base lines, but for this initial model we will assume
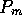 is zero. The holes are place
at 90
is zero. The holes are place
at 90 intervals about the
cross section and every 1 mm along the length.
intervals about the
cross section and every 1 mm along the length. 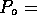 1 kPa (above atmospheric), the fluid flow is
1 kPa (above atmospheric), the fluid flow is

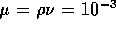 kg/m s (for water, 25
kg/m s (for water, 25 C ),
C ),
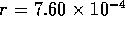 m, and l = 0.1 m.
This yields a flow of
m, and l = 0.1 m.
This yields a flow of 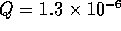 m
m /s and an average fluid velocity
of
/s and an average fluid velocity
of 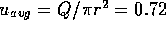 m/s. The Reynolds number
is Re
m/s. The Reynolds number
is Re 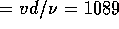 , where
, where 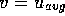 ,
, 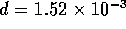 m and
m and 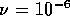 m
m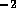 /s, which is below the critical
value Re
/s, which is below the critical
value Re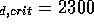 ; therefore we may
assume the flow is laminar. For higher pressures, equation
1 yields Reynolds numbers in the
turbulent range, but the significant resistance offered by the sealed
porous tube reduce the flow rates and maintains laminar conditions. As
we will later show the maximum flow rate is approximately
; therefore we may
assume the flow is laminar. For higher pressures, equation
1 yields Reynolds numbers in the
turbulent range, but the significant resistance offered by the sealed
porous tube reduce the flow rates and maintains laminar conditions. As
we will later show the maximum flow rate is approximately 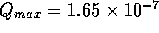 m
m /s, which yields
/s, which yields 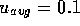 m/s and
m/s and 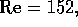 which is certainly laminar. Finally, the entrance region before the
fully developed flow is approximately
which is certainly laminar. Finally, the entrance region before the
fully developed flow is approximately 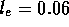 Re
Re 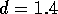 cm;
therefore we can assume the boundary layer is fully develop within the
entire length of the tube.
cm;
therefore we can assume the boundary layer is fully develop within the
entire length of the tube. 
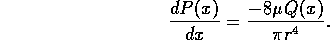
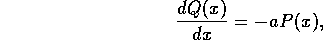

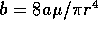 . If we solve this differential
equation with boundary conditions
. If we solve this differential
equation with boundary conditions 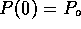 and
and 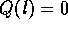 , we
have the head loss as a function of length
, we
have the head loss as a function of length 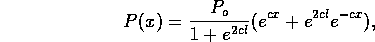
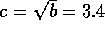 m
m . The head loss in the tube
is not significant in this case as shown in figure 3-2.
. The head loss in the tube
is not significant in this case as shown in figure 3-2. 
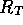 . Following a simplified
convention, we will assume the fluid resistance is given by
. Following a simplified
convention, we will assume the fluid resistance is given by 
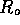 is the resistance
due to the entrance,
is the resistance
due to the entrance, 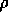 is the
resistance per unit length and l is the length of the tube.
The entrance resistance is given by
is the
resistance per unit length and l is the length of the tube.
The entrance resistance is given by 
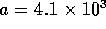 and
and 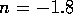 . For the tubes
. For the tubes 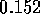 cm in diameter
cm in diameter 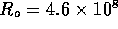 N
N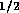 sm
sm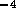 . The resistance per unit length
. The resistance per unit length

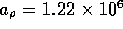 N
N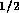 sm
sm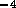 ,
, 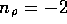 , and d is the inner
diameter. For the tube described above, the resistance per unit
length is
, and d is the inner
diameter. For the tube described above, the resistance per unit
length is 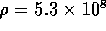 N
N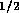 sm
sm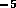 ,
thus the total resistance for the tube is
,
thus the total resistance for the tube is 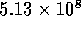 N
N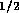 sm
sm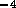 . Using equation
. Using equation 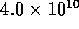 N
N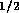 sm
sm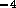 for holes
for holes 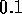 mm in diameter. However with 80 holes/cm and
10 cm of tube, the total resistance is
mm in diameter. However with 80 holes/cm and
10 cm of tube, the total resistance is 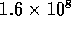 N
N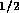 sm
sm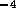 .
. 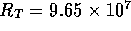 N
N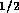 sm
sm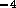 The relation between pressure and flow is again given
by,
The relation between pressure and flow is again given
by, 

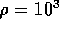 kg/m
kg/m is the fluid density,
is the fluid density, 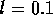 m is the length of the tubes and
m is the length of the tubes and 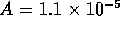 m
m is the total cross sectional area. For this system,
the fluid inertance is
is the total cross sectional area. For this system,
the fluid inertance is 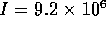 kg/m
kg/m and
the dynamics are given by
and
the dynamics are given by 
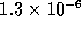 m
m /s in 10 ms under a pressure of 1 kPa. Then the
inertance I would be
/s in 10 ms under a pressure of 1 kPa. Then the
inertance I would be 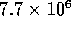 kg/m
kg/m . This is comparable to
the value given for the model. So for switching times on the order of
1 ms, inertance effects become significant.
. This is comparable to
the value given for the model. So for switching times on the order of
1 ms, inertance effects become significant. 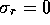 ,
, 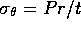 ,
, 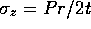 and
and 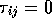 ,
where P is the pressure, t is the wall thickness and
r is the radius. Given the generalized stress-strain relations,
,
where P is the pressure, t is the wall thickness and
r is the radius. Given the generalized stress-strain relations,


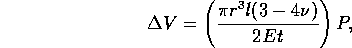
 is Poisson's ratio. Therefore the fluid capacitance
is
is Poisson's ratio. Therefore the fluid capacitance
is 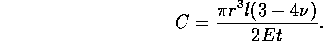
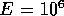 N/m
N/m (approximate for
rubber),
(approximate for
rubber), 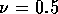 and
and 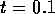 mm,
mm, 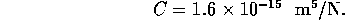
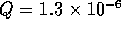 m
m /s, this
capacitance will become significant if the pressure changes more than
1 MPa in a 1 ms. Therefore we will ignore the capacitance.
/s, this
capacitance will become significant if the pressure changes more than
1 MPa in a 1 ms. Therefore we will ignore the capacitance. 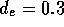 cm and a check valve. Employing
equation 2, this results in a
fluid resistance of
cm and a check valve. Employing
equation 2, this results in a
fluid resistance of 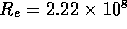 N
N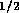 sm
sm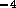 , for a drain line 20 cm in length.
, for a drain line 20 cm in length. 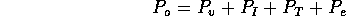
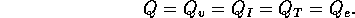
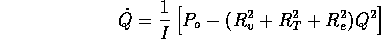
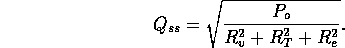
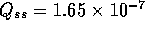 m
m /s. Note the total volume of injected fluid is
/s. Note the total volume of injected fluid is

 equal to half the distance between the tubes. The
mixing time could be approximated, as the time for the fibers at
radius
equal to half the distance between the tubes. The
mixing time could be approximated, as the time for the fibers at
radius 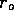 to experience a
certain concentration of fluid. As a simplification we can
approximate the diffusion with the one dimension diffusion equations
to experience a
certain concentration of fluid. As a simplification we can
approximate the diffusion with the one dimension diffusion equations

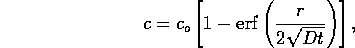
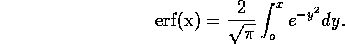
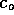 , of course,
decreases as particles diffuse into the liquid. However, as a first
order approximation to the diffusion time, we assume
, of course,
decreases as particles diffuse into the liquid. However, as a first
order approximation to the diffusion time, we assume 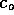 is constant. Then the concentration at
is constant. Then the concentration at 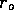 is one-half its initial value
when
is one-half its initial value
when 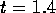 ms for
ms for 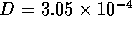 m
m /s (0.1M HCL at 25
/s (0.1M HCL at 25 C ) and
C ) and 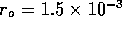 m.
m.


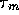 is a time constant which we
will take to be
is a time constant which we
will take to be 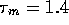 ms (based
roughly on the previous discussion) and
ms (based
roughly on the previous discussion) and 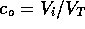 ratio of solute to solvent, where
ratio of solute to solvent, where 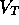 is the total volume of the actuator,
is the total volume of the actuator, 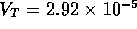 m
m .
. 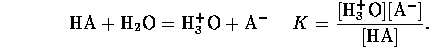

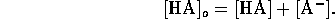
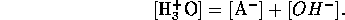
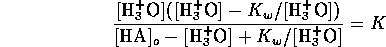
 from water is negligible
compared to that from the acid, hence
from water is negligible
compared to that from the acid, hence 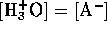 . We may
assume that for strong acids there is complete dissociation; that is
. We may
assume that for strong acids there is complete dissociation; that is
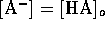 , which yields the trivial result
, which yields the trivial result

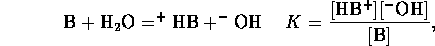

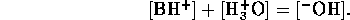

 from self-ionization of water is
negligible, hence
from self-ionization of water is
negligible, hence
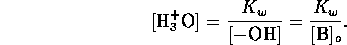
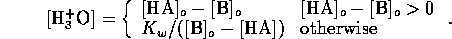
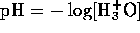 , we have
, we have
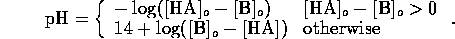

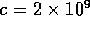 s/m
s/m .
Thus for fibers 10
.
Thus for fibers 10 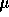 m in diameter contract in approximately 0.1 s.
This can also be approximated to the first order by
m in diameter contract in approximately 0.1 s.
This can also be approximated to the first order by

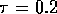 , pH is the pH in the fiber
and pHs is that in the
solvent. Notice this time constant is substantially slower than the one
given in equation 3. Therefore we will ignore the lag due
to mixing and consider only the diffusion within the fiber as the major
delay.
, pH is the pH in the fiber
and pHs is that in the
solvent. Notice this time constant is substantially slower than the one
given in equation 3. Therefore we will ignore the lag due
to mixing and consider only the diffusion within the fiber as the major
delay.
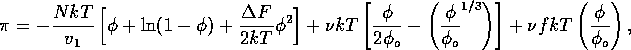
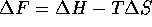 represents the difference
between the free energies of a polymer segment-segment
and polymer-solvent interaction, and
represents the difference
between the free energies of a polymer segment-segment
and polymer-solvent interaction, and
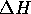 and
and 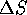 are the enthalpy and entropy respectively.
In equilibrium, the osmotic pressure is zero.
Thus by solving the above equation, we can theoretically
compute the fiber force. However because of its complexity and
because of the availability of empirical data, we can describe the
contraction of the fiber with the simple model shown in figure 3-4.
The intrinsic force per unit area is
are the enthalpy and entropy respectively.
In equilibrium, the osmotic pressure is zero.
Thus by solving the above equation, we can theoretically
compute the fiber force. However because of its complexity and
because of the availability of empirical data, we can describe the
contraction of the fiber with the simple model shown in figure 3-4.
The intrinsic force per unit area is 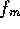 is approximately
is approximately
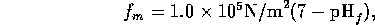
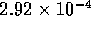 m
m ,
the intrinsic force is
,
the intrinsic force is 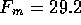 N(7-pH
N(7-pH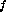 ).
Also the intrinsic stiffness is
).
Also the intrinsic stiffness is
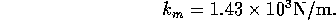


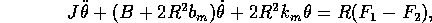


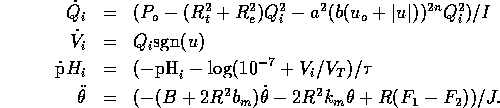
 . In order simplify this problem further let us
assume a single-input single-output system, by taking the co-contraction
of the actuators as an offset force and controlling position through feedback
through a single actuator. With these initial assumptions let us write the system
equations in the form
. In order simplify this problem further let us
assume a single-input single-output system, by taking the co-contraction
of the actuators as an offset force and controlling position through feedback
through a single actuator. With these initial assumptions let us write the system
equations in the form



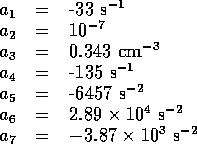
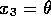 using the simplified model
presented above. We would also like the controller to
maintain zero tracking error in the presence of modeling errors. Therefore,
we will design a non-linear sliding mode controller.
using the simplified model
presented above. We would also like the controller to
maintain zero tracking error in the presence of modeling errors. Therefore,
we will design a non-linear sliding mode controller.
 . Therefore let us initially
assume the inertia can be neglected, and produce a controller based on the
reduce third order system,
. Therefore let us initially
assume the inertia can be neglected, and produce a controller based on the
reduce third order system,
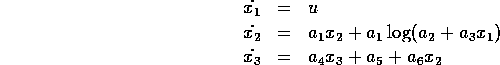

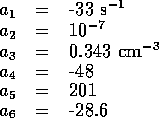 <
<
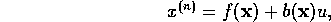
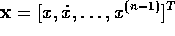 ,
can be derived by differentiating the equation for the joint
angle three times.
,
can be derived by differentiating the equation for the joint
angle three times.
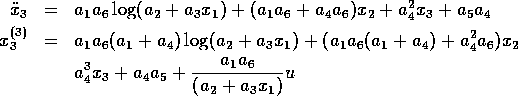
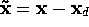 be the tracking error on
be the tracking error on 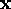 and
define the sliding surface to be
and
define the sliding surface to be
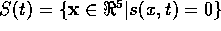 , where
, where
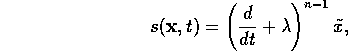
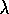 . Hence
. Hence

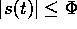 , then
, then
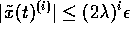 . We must now design a controller
such that for all
. We must now design a controller
such that for all 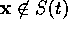 ,
,
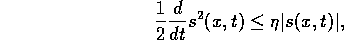
 .
The estimation of f is given by
.
The estimation of f is given by 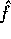 and the bounds on the error is
and the bounds on the error is

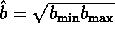 where
where 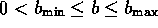 . If we let
. If we let
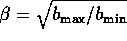 , then
, then

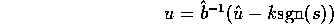
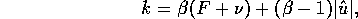
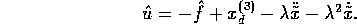
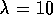 s
s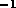 to be approximately equal to the natural
frequency of the system while the estimate errors to be approximately 10% the nominal values.
to be approximately equal to the natural
frequency of the system while the estimate errors to be approximately 10% the nominal values.
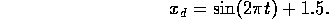
 Fourth and fifth order sliding mode controllers were attempted to compensate for the link
inertia and fluid inertance, but were found to be numerically unstable in the calculation
of the higher order derivatives. Numerical filters corrected this problem, though the
simulation times became unacceptable long. A more judicious choice of numerical parameters
could possibly correct this problem.
Fourth and fifth order sliding mode controllers were attempted to compensate for the link
inertia and fluid inertance, but were found to be numerically unstable in the calculation
of the higher order derivatives. Numerical filters corrected this problem, though the
simulation times became unacceptable long. A more judicious choice of numerical parameters
could possibly correct this problem.




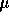 m), while using UV induced transectional cross-linking to
increase strength. These and other innovations should
allow faster response times for practical actuator development and controller
design.
m), while using UV induced transectional cross-linking to
increase strength. These and other innovations should
allow faster response times for practical actuator development and controller
design.