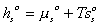
System: (Polymer gel network + solvent inside) inside the control volume (c.v.)., i.e., the control volume is changing as the get network is expanding due to absorbing the surrounding solvent fluid.
Modeling Assumptions:
Consider the polymer gel network inside the c.v. as shown above. The c.v. is surrounded by the solvent fluid at constant temperature, To, and constant pressure, Po. As the solvent fluid enters the c.v., the c.v. expands, and the state of the system inside the control volume at an instant of time can be themodynamically described by
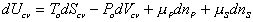(1)
where
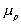is the chemical potential of polymer inside the c.v.,
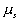is the chemical potential of solvent inside the c.v.,
Since the number of mole of polymer inside the c.v. is fixed, the third term on
the right hand side (RHS) is zero, i.e.,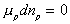 
.
In addition, the second term on the RHS, PodVcv, represents the
differential expansion work done by the c.v.. Assuming both the polymer and
the solvent to be incompressible, then PodVcv = 0 since the expansion of
c.v. alone is exactly cancelled by the flow work done by the solvent flowing
into the c.v.. The Equation (1) then simplies to
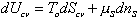(2)
With the assumption of quasi-staticity of the process, then the system inside the c.v. may be treated as the lumped parameter multiport capacitance with the relation
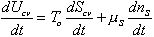(3)
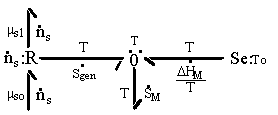
The first term on RHS represents the effects of heat transfer, entropy transfer due to convection and the entropy generation due to irreversibility. The second term on RHS represents the chemical energy brought in by the incoming surrounding solvent. The bond graph representation of the system is
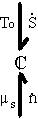
The constitutive relations describing the equilibrium state of the polymer-solvent gel network system has been derived by Flory, and it will be base of the multiport capacitance model.
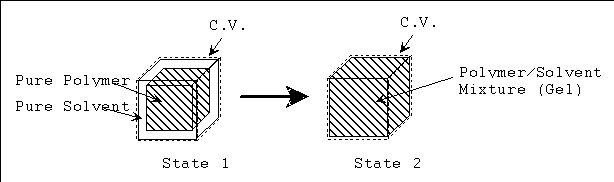
The process from state 1 to state 2 is therefore entropy generating run-down mixing process, and the changes in thermodynamic properties of control volume due to such mixing process are described by Flory.
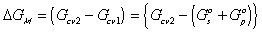
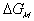is the change in Gibbs free energy of c.v. due to mixing,Similarly,
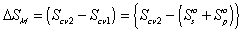
The Gibbs free energy change of c.v. by mixing of polymer and solvent is
considered to be due to two effects; combinatorial effect,
,
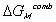and polymer-solvent contact effect,
.
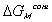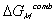accounts for the many different conformations the amorphous polymer may adopt,
and
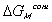accounts for the effects of non-randomness induced by intermolecular
interactions.
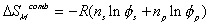
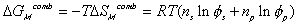
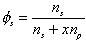
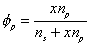
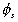is the volume fraction of solvent,
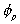is the volume fraction of polymer,Vp = x Vs.
The intermolecular interaction also involves enthalpy change.
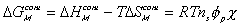
where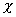 
is the Flory-Huggins polymer-solvent interaction paramter.
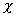is a temperature dependent dimensionless quantity which characterizes
polymer-solvent interactions, and can be expressed in the form
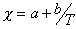
where a and b are temperature independent quantities.
Then,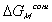 
can be written as
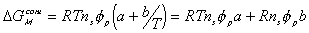
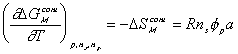
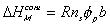
Note that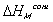 
represents the thermal energy generated
due to the mixing process, and thus
can be modelled as the heat transferred to the surrounding solvent environment
while maintaining isothermal condition.
Combining both the combinatorial and polymer-solvent contact effects, we have
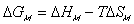
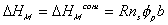
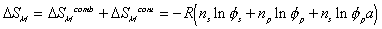
The change in Gibbs energy can be viewed as the energy lost due to
entropy generating process, and for quasistatic mixing/diffusion process, the
rate of change of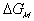 
can be written as
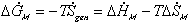
Also,
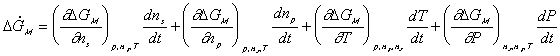
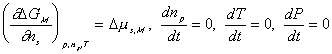
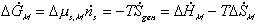
This entropy generation process can be modelled as a 3-port resistance field driven by the chemical potentials of solvents across the gel's control volume boundary.
Since the entropy and Gibbs free energy of gel system inside the control volume at are
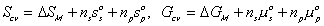
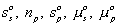are constant during the process, the rate of change of Scv, and
Gcv with respect to time are
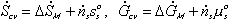
Combining the above results, we then have
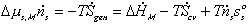
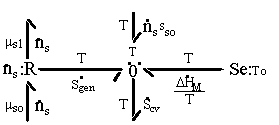
Note that the resistive R field in the bond graph is presented such that the kinetics of the solvent flow may depend on both the chemical potentials of solvent outside and inside the gel rather than just the net difference in chemical potential across the gel boundary. The phenomenological description of diffusion/mixing process is also needed here to relate the rate of solvent flow into the control volume to the chemical potentials of solvent. For initial investigation, a simple description of non-electrolyte solvent diffusion is employed;
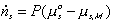
where P represents the permeability coefficient.
According to Flory's work, deformation of polymer gel network may be modelled
as consisting of two step processes; first, expansion due to free swelling and
second, stretching at constant volume, without changing the enthalpy of the gel
system. Based on statistical theory of rubber elasticity where the end-to-end
distances of the polymer chains can be described by the Gaussian distribution,
the Gibb's free energy change,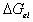 
, and the entropy change,
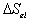, due to elastic deformation are described by
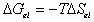
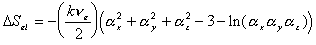
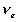is the effective number of chains in the gel,
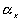represents the elongation factor in x-axis; 
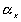= length/free length in x-axis
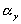represents the elongation factor in y-axis
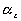represents the elongation factor in z-axis.
Assume that the network formed at volume Vo is subsequently swollen
isotropically by a diluent to a volume V such that the volume fraction
of polymer is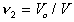 
. In the subsequent deformation due to stretching,
the volume is assumed constant. Letting
,
,
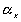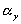and
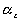represent the changes in dimensions resulting from the combination of
swelling and elongation, we have therefore that
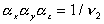is constant during the elongation. Considering only a simple elongation in
the x-direction, let
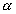represent the length in this direction relative to the swollen, unstretched
length Lo,s = (V/Vo)1/3 Lo, since the swelling is isotropic,
i.e.,
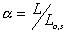
Then
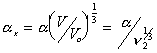
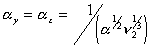
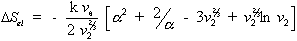
For the deformation process during swelling and stretching, the heat of
deformation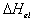 
is considered negligible,
and therefore the Gibbs free energy is then
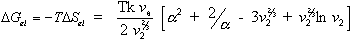
At contant temperature as assumed previously,
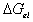is a function of the number of mole of solvent in the c.v. and the elongation,
i.e.,
.
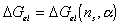Taking the above result by Flory, then the rate of change of Gibb's free
energy with respect to time can be represented as
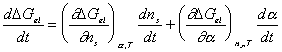
In addition,
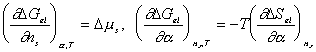
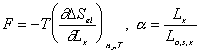
After combining the above result and little algebraic manipulations, we have
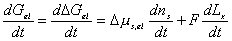
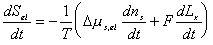
Since
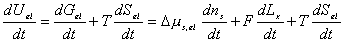
the bondgraph structure for multiport capacitance due to rubber elasticity is
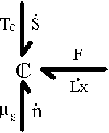
The validity of the Flory's assumption of modelling the deformation process as two step process should be checked. Specificially, researchers have observed that elongation of elastomeric polymer gel increases the swelling degree of the gel. In other words, stretching decreases the osmotic pressure of solvent inside the gel whereas compressing has reverse effect. Similarly, it also implies that the chemical potential of the solvent inside the gel should decrease when stretched and increase when compressed. However, it is found that the Flory's model does not predict such behavior according to the our preliminary results, but in fact predicts reverse effect. The validity of our results as well as the Flory's model of deformation effect need to be investigated further.
The above theory on rubber elasticity of swelling gel by Flory is based on the complex statistical theory which remarkably relates how the molecular structure of elastomer responds to an applied strain to the macroscopic deformation behavior. However, this theory still offers only qualitative approximation to the actual behavior of elastomer, mainly due to the assumption that end-to-end distances of the chains can be described by the Gaussian distribution. Given such deficiency of statistical model, the purpose of this section is to describe the gel's elasticitic behavior with simpler mechanical analog; the springs.
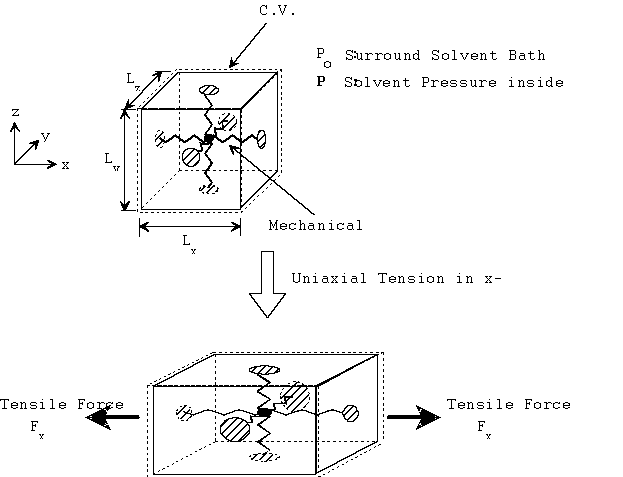
Let's consider a unit cube of the isotropic gel where the opposite faces of the cube are linked by a mechanical spring in all three axes. These mechanical springs represents the rubber elasticity of the gel elastomer, and therefore their rest lengths are the linear dimensions of gel when it is fully contracted and free of external stress. In addition, the elastomer itself occupies a constant finite volume. Defining the control volume as the space occupied by the solvent only, the mechanical springs inside the control volume then may be treated as volume-less pure mechanical spring elements, and let's assume such control volume is still an isotropic cube for simplicity. Then, static force balance at each face of the control volume relates the pressures of solvent to the tensile force as
Px Ax = Po Ax + Fx
Py Ay = Po Ay + Fy
Pz Az = Po Az + Fz
Ax = Ly Lz
Ay = Lx Lz
Az = Lx Ly
Assuming the uniform pressure P inside the control volume,
Px = Py = Pz = P
and modeling the mechanical spring as simple Hookean spring, the spring forces are then
Fx = K Lx
Fy = K Ly
Fz = K Lz
For the simple case of uniaxial tension in x-axis, Ly = Lz due to isotropy of gel, and thus
V = Lx Ly Lz = Lx Ly2
where V is the volume of the solvent inside the control volume.
Combining above results, we get
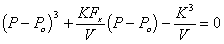
where the solvent pressure P can be solved as a function of Fx and V.
Modeling the effect of rubber elasticity as purely mechanical, the change in chemical potential of solvent due to the rubber elasticity is then
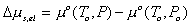
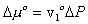
where v1o is molar volume of pure solvent. Combining above two results, we get
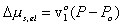
For the case of free swelling, the effect of rubber elasticity is
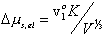
and this result is consistent with Flory and Treloar.
According to above results based on simple mechanical spring, the effect of elongation/compression on the swelling degree of gel is in agreement with the observed behavior. The change in chemical potential of solvent inside the gel is directly proportional to the osmotic pressure, and both the solvent's chemical potential and osmotic pressure is decreased when elongated and increased when compressed. Before proceeding, however, one should note the limitations of this simple mechanical model, namely the lack of coupling between the mechanics and thermodynamics of the mechanical spring. With real elastomer, there is thermal-mechanical energy conversion, as Flory's model describes in terms of entropy change due to deformation. For instance, when the elastomer is stretched, it is observed to grow warmer. Such energy coupling behavior is neglected in this simple pure mechanical spring model, and the importance of this coupling effect needs to be investigated further in order to validate this simple model.
Combining the previous results on mixing/diffusion process and the deformation process, we then have
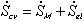
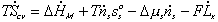
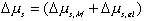
One should note that the mechanical force contribution in above equation is based on Flory's rubber elasticity model, and it does not show up explicitly in junction structure since it is embedded in the nature of multiport capacitance. Applying the integral causality to chemical and mechanical ports to the multiport capacitance field, the bond graph representation of the overall system is then
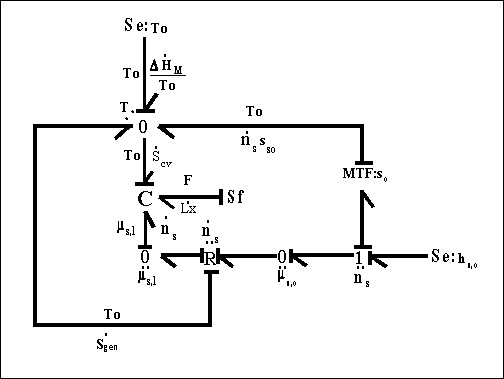
Note that for the surrounding solvent
