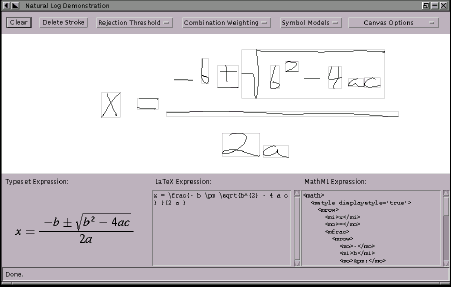
This page describes our approach for converting a handwritten mathematical expression into an equivalent expression in a typesetting command language such as TeX or MathML. We have used these ideas to build a demonstration system in Java which recognizes simple expressions written with a pen tablet. A screen image of the system is provided below. The white area is for pen input, and output is provided below in three forms, from left to right: a typeset image, TeX, and MathML (Typesetting provided by WebEQ).

We divide the recognition problem into three modular subproblems called isolated symbol classification, stroke set partitioning, and parsing. This division has the advantage that each subproblem can be solved and its performance evaluated essentially independent of the others, so that improvements can be made in each area while still maintaining the integrity of the entire system.
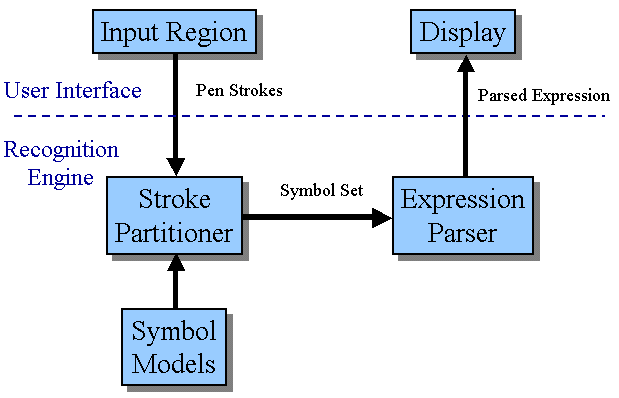
Recognition is performed in two discrete stages, indicated in the diagram below. First, the strokes are partitioned into symbols by the stroke partitioner. Then, the identity of the symbols and the structure of the expression is determined by the parser. Symbol models, estimated from examples of handwriting, are used by the partitioner in order to decide how likely it that a particular set of strokes constitutes a distinct symbol. After recognition is complete, the user interface displays the resulting expression.
One important aspect of this division is that hard decisions are made at each stage, so that new information cannot change the results of earlier processing. This has the advantage that it makes the algorithm fast, since it reduces the number of possibilities that it considers in its interpretations. However, it does have the disadvantage that higher-level information, such as the structure of the interpreted expression, cannot change lower-level decisions, such as the stroke set partitioning.
One of the basic problems in handwriting recognition is to take a set of strokes and determine, out of context, which symbol it best represents. To solve this problem we use a statistical approach, creating a single Gaussian model for each symbol class based on examples of a single user's handwriting. The example symbols were preprocessed and then used to estimate the model parameters for each class of symbol in a training phase. Then, during the processing of an unrecognized expression, potential symbols are similarly processed and compared to the models for classification.
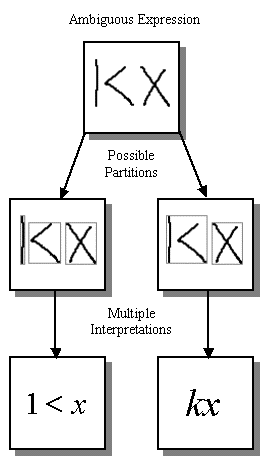
Even if one is provided with a perfect symbol classification algorithm, there is still no way of knowing, a priori, which strokes in an expression should be combined together into symbols or even how many symbols are present. Consider the example of the ambiguous expression in the diagram on the right. In this example, it is unclear whether there are three symbols present, 1 < x or whether there are just two, kx. The best interpretation of the overall expression depends on how the strokes are partitioned.
Therefore, the capabilities of the symbol classifier need to be used within a larger framework to determine the quantity and locations of the symbols present in an expression. In printed text, such as mathematics, each pen stroke belongs to a distinct symbol; i.e. no two two symbols share a stroke. Thus, solving the partitioning problem for printed text is equivalent to finding the best grouping of a set of strokes into a set of symbols, called a partition of an expression.
In general, the number of possible partitions of a set of strokes into symbols is exponential in the number of strokes. Therefore, some constraint on the search is necessary if the algorithm is to take a reasonable amount of time to finish. One typical solution is to use the time ordering of the strokes as a constraint; that is, only consider symbols which consist of strokes which were drawn one after the other. While this is efficient, it prevents the user from changing their expression as they write, say by turning a minus sign into a plus sign.
Instead of a stroke ordering constraint, we choose to use a geometric constraint by only exploring possibilities which are covered by a minimum spanning tree over the strokes. This tree is defined to be the set of edges connecting the centers of each stroke, such that there are no cycles in the tree, there is a path between every pair of strokes, and the sum of the lengths of the edges is minimized.
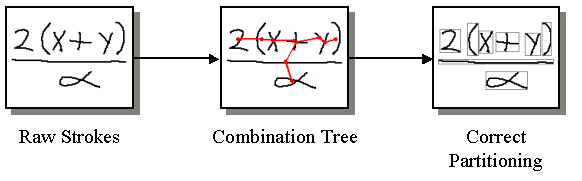
Once a minimum spanning tree is found for a set of strokes, the search for an optimal partition can be constrained by considering only partitions that form connected subtrees in the MST. In the example shown below, there are three two-stroke symbols, the x, the y, and the +. To correctly partition the expression, it is necessary to consider each of these stroke-pairs as a possible two stroke symbol. This does in fact occur, because these pairs are connected in the MST. The 2 and the alpha, on the other hand, are not considered as possibly belonging to the same symbol since they are not connected.
Once the expression has been correctly partitioned into symbols, there still remains the problem of determining which characters the symbols represent and deciding on the structure of the resulting typeset expression. This can be done using a geometric grammar whose elements are inspired by the atomic elements of TeX's typesetting engine. In this grammar, each character belongs to a single grammar type and combines with other characters in well defined ways based on simple relationships between their bounding boxes. In addition, simple characters also have a baseline which aids in determining when a character is superscripted.