
The Recognition of Material Properties for Vision and Video Communication
MIT2000-02
Progress Report: July 1, 2000–December 31, 2000
Edward H. Adelson
Project Overview
How can we tell that an object is shiny or translucent or metallic by looking at it? Humans do this effortlessly, but machines cannot. Materials are important to humans and will be important to robots and other machine vision systems. For example, if a domestic cleaning robot finds something white on the kitchen floor, it needs to know whether it is a pile of sugar (use a vacuum cleaner), a smear of cream cheese (use a sponge), or a crumpled paper towel (grasp with fingers).
An object’s appearance depends on its shape, on the optical properties of its surface (the reflectance), the surrounding distribution of light, and the viewing position. All of these causes are combined in a single image. In the case of a chrome-plated object, the image consists of a distorted picture of the world; thus the object looks different every time it is placed in a new setting. Somehow humans are good at determining the "chromeness" that is common to all the chrome images.



The image of an object with a chrome-like surface depends on the object shape and on the surrounding distribution of light in the room. Every image is different, but something (the "chromeness") is the same.
Progress Through December 2000
To simplify the problem, we assume the object’s shape is known, while its reflectance and the surrounding light distribution are unknown. For the simplest geometry we are use images of spheres. These images may be taken from the natural world, by photographing spheres in real-world settings, or they may be synthetic images generated by computer graphics. Each image can be considered to be a sample from an image-generating process in which a reflectance and a real-world scene are randomly chosen. In principle, any image could be interpreted as a chrome sphere placed in the right scene; one could arrange the lights in the room to form a sphere image that looked exactly like that of a ping-pong ball. However, this never happens in real life, because real-world scenes have certain statistical properties. We can take advantage of this constraint and learn what kind of images commonly occur for a given reflectance.

Three spheres with different reflectance properties.
The problem of material recognition has some similarities to that of visual texture recognition. Note that the problems are not the same: in the case of texture, the image is assumed to result from a stationary process that is the same over the whole image, whereas in the case of spheres the image qualities are quite non-stationary. However, we can adapt ideas from texture. Recently it has been shown that the statistics of wavelet coefficients (i.e., .the values in subbands) are particularly useful for analyzing texture, especially when combined with pixel intensity statistics. We unwrap an annulus from a sphere image, transforming it into a somewhat uniform texture and extract various wavelet and intensity statistics. We use these values as features in a statistical learning system. We use support vector machines (SVMs) for classification because they tend to generalize well given a limited number of training samples and a large number of features.
To test the accuracy of classification based on different combinations of statistics using only a small total number of data points, we performed a variant of leave-one-out cross-validation. We classified the six images corresponding to each illumination using a classifier trained on the images corresponding to the other eight illuminations. By repeating this process for each of the 9 illuminations, we obtained a total of 54 test cases, one for each rendered image. Classification based on five or more statistics produced accuracies as high as 53 of 54 correct.

Flow diagram for classifying spheres according to reflectance.
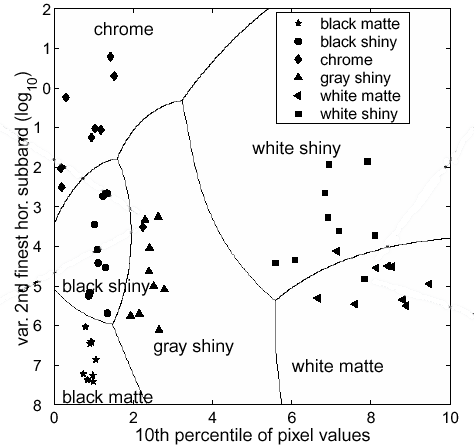
Classification results using two features.
We have also developed a separate algorithm that estimates the shape, reflectance parameters, and lighting for glossy, convex objects. This algorithm uses the outline of the object to compute an estimate of the shape of the object. The lighting direction and reflectance parameters are then found by adjusting them to minimize the difference between the image of estimated shape rendered using those parameters and the actual image of the object.
Research Plan for the Next Six Months
We will improve the performance of our reflectance estimator and apply it in a more practical setting. Currently, the estimator is limited to images of spheres. We plan to apply it to surfaces other than spheres. Our method generalizes naturally to surfaces of other convex geometries, because under the assumption of distant illumination, the observed brightness of a surface patch depends only on its orientation relative to the viewer. Second, we will investigate principled manners to choose the best statistics for classification from the family defined by the distributions of pixel intensities and wavelet coefficients.
We also plan to improve the robustness of the outline-based algorithm described above. It works well for small "blobby" objects, but the shape model has limited freedom. We will extend the model and estimation procedure to work on a broader class of shapes. We will also develop a more principled process for estimating the lighting direction.