How can we tell that an object is shiny or translucent or metallic by looking at it? Humans do this effortlessly, but machines cannot. Materials are important to humans and will be important to robots and other machine vision systems. For example, if a domestic cleaning robot finds something white on the kitchen floor, it needs to know whether it is a pile of sugar (use a vacuum cleaner), a smear of cream cheese (use a sponge), or a crumpled paper towel (grasp with fingers).

An object’s appearance depends on its shape, on the optical properties of its surface (the reflectance), the surrounding distribution of light, and the viewing position. All of these causes are combined in a single image. In the case of a chrome-plated object, the image consists of a distorted picture of the world; thus the object looks different every time it is placed in a new setting. Somehow humans are good at determining the "chromeness" that is common to all the chrome images.

Figure 1: The image of an object with a chrome-like surface depends on the object shape and on the surrounding distribution of light in the room. Every image is different, but something (the "chromeness") is the same.

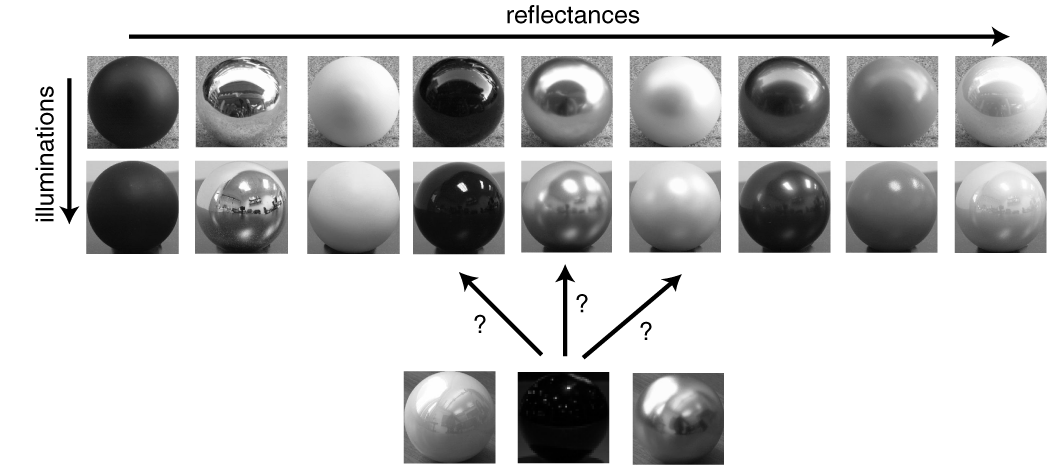
Figure 2: The problem addressed by our classifier, illustrated using a database of photographs. Each of nine spheres was photographed under seven different illuminations. We trained a nine-way classifier using the images corresponding to six illuminations, and then used it to classify individual images under the seventh illumination. The classification algorithm uses image data only from the surface itself, not from the surrounding background.

Over the past six months, we generalized this algorithm and quantified its performance. A paper we presented at the Workshop on Statistical and Computational Theories of Vision at the International Conference of Computer Vision compares several machine learning technique for reflectance estimation. We found that support vector machines outperform other classification techniques in this problem, particularly when the amount of available training data is small compared to the number of reflectance classes and the number of features utilized. The same paper establishes an automatic, data-driven method for choosing a set of features that will lead to robust classifier performance given limited training data. Our automatic feature selection method outperforms simple alternatives such as principle components analysis, but does not match the effectiveness of hand selection, leaving room for further improvement.

We studied the sensitivity of various observed surface image statistics to reflectance using a parameterized reflectance model from computer graphics, due to Ward. The Ward model,

provides a functional form for the bi-directional reflectance distribution function with three free parameters: r d, which specifies intensity of diffuse reflectance, r s, which specifies the intensity of specular reflectance, and a , which specifies the width of the specular lobe. We compared the changes in the value of each statistic due to changes of each reflectance parameter to those due to changes in illumination (Figure 3). We found that these relative sensitivity values depend heavily on the statistics of the illumination, implying that reflectance estimation depends on the statistics of natural illumination.

Finally, we generalized our reflectance classification algorithm to handle non-spherical surfaces. When a distant viewer observes a convex surface under distant illumination, the brightness of a surface point depends only on local surface orientation. One can therefore map any observed surface of known geometry to an equivalent sphere of the same reflectance properties under the same illumination by matching corresponding surface normals. Figure 4 shows several examples of such mappings. Computing image features on these mapped images proves challenging because some surface normals are sparsely sampled or absent in the observed image. We used normalized convolution, a technique developed by Knutsson and Westin, to compute wavelet coefficients of these images. This work will appear in a workshop at the Conference on Computer Vision and Pattern Recognition in December.

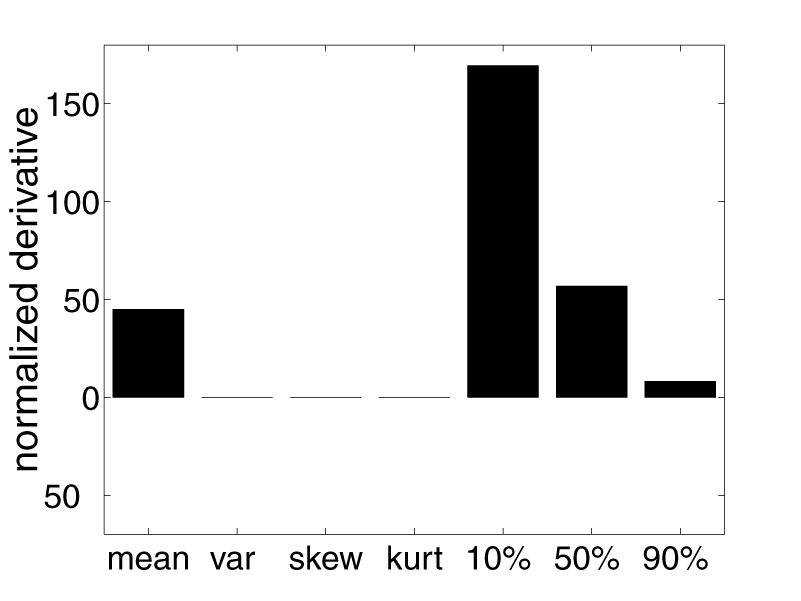
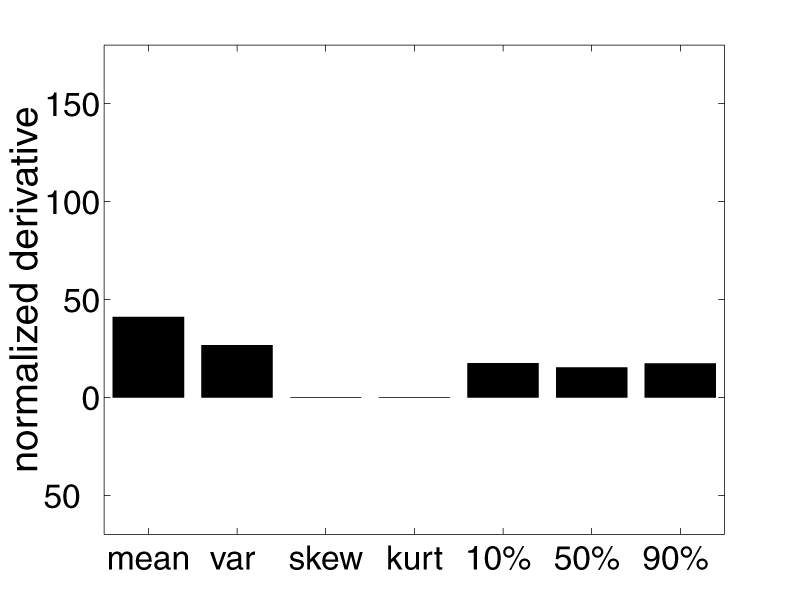
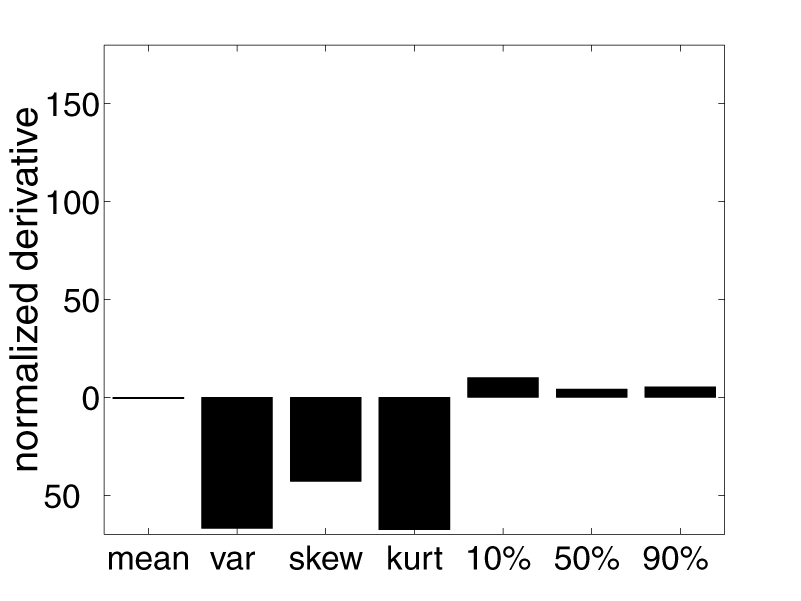
Figure 3: Each bar chart shows the sensitivity of one image statistic to changes in one reflectance parameter, computed as the ratio of the derivative of the statistic with regard to the parameter and the standard deviation of the statistic across illuminations.

Figure 4: Images of surfaces of three geometries, each mapped to an equivalent sphere of the same reflectance and illumination.

Figure 5: Three spheres with identical reflectance properties. Sphere A is rendered under point source illumination, while spheres B and C are rendered as they would appear at two points in the real world.

Humans succeed at recognizing reflectance properties of materials such as metal, plastic, and paper under a wide range of viewing conditions despite the fact that different combinations of illumination and reflectance can produce identical images. Under ordinary viewing conditions, an observer can draw on multiple sources of information to determine surface reflectance properties such as color, gloss, etc. Potentially useful cues include motion, stereo, knowledge of illumination conditions, and familiarity with the object. In order to test whether human subjects can judge reflectance properties in the absence of such cues, we measure their ability to estimate reflectance properties from isolated images of single spheres. In other words, we see how good humans are at the specific task we are trying to solve by computer.

Researchers in computer vision and graphics often assume that point source illumination simplifies the process of reflectance estimation. Figure 4 shows synthetic images of three identical spheres under different illuminations. Sphere A was rendered under point source illumination, while spheres B and C were rendered under photographically-captured real-world illumination. The impression of the material quality is clearer in B and C than in A. We show that humans in fact estimate reflectance more reliably under complex realistic illumination than under simple synthetic illumination.

Why might real-world illumination facilitate reflectance estimation? In the real world, light is typically incident on a surface from nearly every direction, in the form of direct illumination from luminous sources or indirect illumination reflected from other surfaces. The illumination at a given point in space can be described by the spherical image acquired by a camera that looks in every direction from that point. We have recently shown that the spatial structure of such real-world illumination possesses statistical regularity similar to that of natural images. Like our computer system, humans might exploit such regularities to solve the otherwise ill-posed reflectance estimation problem. We use a surface reflectance matching task in order to measure how good subjects are at estimating surface reflectance under various natural and artificial patterns of illumination.

In our surface reflectance matching task, subjects were presented with two spheres that had been computer rendered under different illuminations. Their task was to adjust the surface reflectance of one sphere (the "Match") until it appeared to be made of the same material as the other sphere (the "Test") despite the difference in illumination. The spheres were viewed against a standard random-check background that was identical for all stimuli and thus provided no information about the illumination. Example matching stimuli are shown in Figure 5.

We found that humans perform the task effectively under different natural illuminations. Figure 6 summarizes the results under one particular test illumination. In general, humans perform the matching task more effectively under natural illumination than under synthetic illumination. Our psychophysical work will appear in a workshop at the Conference on Computer Vision and Pattern Recognition in December.

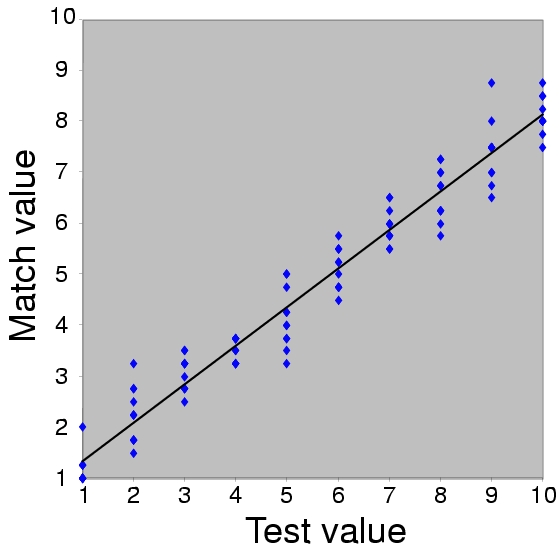
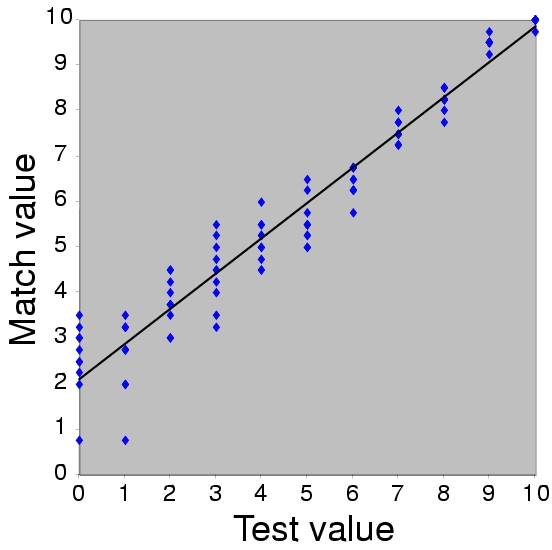
Figure 6: Match values of the parameters as a function of Test values, averaged across four subjects, for one of the real-world illuminations. Each point corresponds to one Test stimulus. The line represents the best linear model. (A) Matches for the parameter controlling the amount of specular reflection. (B) Matches for the parameter controlling width of the specular lobe, which corresponds to the roughness of the surface. Units are arbitrary.

Our computational and our psychophysical results suggest that statistical regularities in real-world illumination help make the reflectance estimation problem tractable. By analyzing a set of natural illumination maps, we have quantified some of these statistical regularities. One can measure the illumination incident from every direction at a point in the real world using a camera located at the point of interest. By combining photographs taken by that camera in every direction, one can compose a spherical illumination map fully describing illumination at that point. We analyzed a set of high dynamic range spherical illumination maps in the image domain, the frequency domain, and the wavelet domain, and compared the results to those reported in the natural image statistics literature. The results will appear in the Conference on Computer Vision and Pattern Recognition in December.

In our previous report, we mentioned an algorithm which simultaneously recovers geometry, illumination, and reflectance of a surface for a limited class of objects. We have extended this contour-based algorithm for recovering object shape and reflectance in several ways. We developed procedures for finding better initial estimates of the reflectance parameters. Initial estimates of the surface roughness are computed by analyzing the size and intensity of specular lobes. The algorithm was also extended to segment a shape into segments with non-overlapping surface normals. We will use this segmentation in the future for estimating surface properties. In order to introduce insights from the study of natural illumination statistics in this context, we also created a system to allow users to "paint" light onto a sphere, then illuminate an object with that light.

First, we wish to refine our techniques for reflectance estimation under complex geometry and to attack the problem of reflectance estimation when geometry is unknown, taking a major step towards applying our algorithms to practical vision problems.

Second, we hope to develop an analytic framework for reflectance estimation, expressing image statistics in terms of illumination statistics and reflectance. This will place our algorithms on a firmer theoretical foundation and will allow us to optimize our choice of image features.

We plan to complete the psychophysical experiments on reflectance estimation described above, producing a more quantitative measure of human performance at this task and identifying the characteristics of illumination that lead to systematic biases in humans. We also hope to extend these experiments to study perception of material properties other than reflectance.