Model Reduction for Human and Animal Locomotion

MIT2001-08

Progress Report: January 1, 2002—June 30, 2002

Jovan Popovic

Project Overview

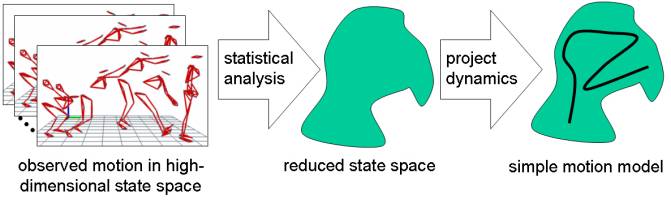
Complexity of existing mathematical models inhibits the analysis and the automatic animation of human and animal motion. Current techniques rely on numerical simulations of highly nonlinear differential equations in high-dimensional spaces. A motion with such large-scale dynamics is difficult to control because of the sheer size of its control space. We are developing a method for constructing simpler mathematical models of lower dimensionality. The simplification consists of two steps: state-space reduction and model projection. The state-space reduction relies on statistical analysis of real-world observations to reduce the dimensionality of the original state space. The model projection constructs a new mathematical model on the reduced subspace by projecting the original equations of motion. The simplification will enable automated animation of complex mechanical systems.

Progress Through June 2002

The Lagrange formulation is a three-step recipe for deriving motion models of mechanical systems. First, select a state space that describes configurations of a mechanical system. For example, the state space for a skeleton would describe joint angles and the pose of the root joint. Second, write the Lagrangian function on the state space. For example, the Lagrangian for skeletal motion is the difference between the kinetic and the potential energy of the skeleton. Third, apply the Euler-Lagrange equations to generate the equations of motion.

The Lagrangian recipe generates appropriate equations for all differentiable state spaces. For skeletal motion, this generality implies that the same recipe produces low-dimensional motion models for Lagrangians on simple skeletons and high-dimensional models for Lagrangians on intricate skeletons. Eliminating the joints simplifies the mathematical model of motion. Although skeleton simplification is a standard preprocessing practice in computer animation, it has two significant drawbacks. First, it ties simplification to joint-angle representation and cannot reveal structure in alternative representations such as saggital elevation angles or marker data recorded by a motion-capture system. Second, it provides no mechanism for identifying dimension of the reduced state space.

We use principal component analysis to reduce the dimensionality of a configuration space. Our motion-capture system provides the data needed for this analysis. A mathematical model defines the equations of motion that describe the evolution of a skeleton in the reduced space. We derive these equations by the standard Lagrange recipe, after projecting the Lagrangian of the skeleton to the reduced space.

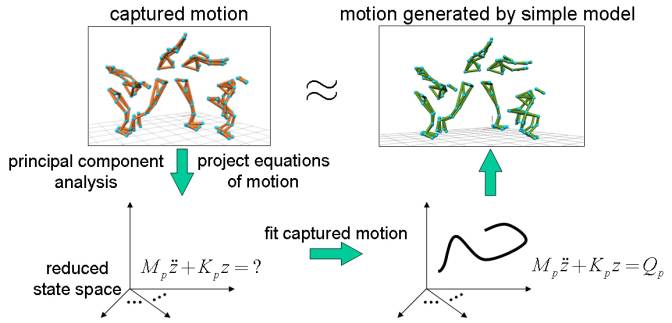Figure 1. A fitting procedure estimates the parameters of the simple model (the generalized forces) to approximate the original motion.

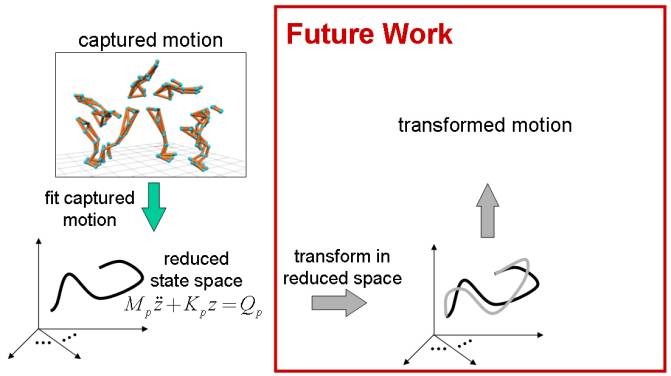
A simple mathematical model enables physically based transformation of recorded motion. A motion transformation technique should produce a new motion that satisfies novel constraints while retaining the detail and style of the recorded motion. For example, if we record a human broad jump, we might want to elongate or shorten the jump without loosing the style of the original motion. This problem can be formulated as a constrained optimization, which minimizes the difference between the original and transformed motion subject to Newtonian constraints, which make the resulting motion physical, and animation constraints, which describe the requirements for new motion. While large-scale dynamics of skeletal motion prevents robust convergence of the optimization in the high-dimensional state space, a simple mathematical model enables convergence by approximating Newtonian constraints.

We completed the first step of a new motion transformation technique. In this step, the fitting procedure estimates the parameters of the simple model (the generalized forces in the reduced space) to approximate the original motion, as shown in Figure 1. The new motion exhibits small stretching and sliding artifacts, which result from reducing the original 123-dimensional state space to the new 10-dimensional space, but otherwise the approximated motion looks natural and close to the original, as shown in Figure 2.

Figure 2 The difference between original motion in orange and the estimated motion in green.

Research Plan for the Next Six Months

In the reduced state space, a constrained optimization can transform a motion described by the simple mathematical model. We will implement these steps in the next six months to complete our motion transformation technique.