Monitoring Network Routing
and Traffic with Low Space
MIT2001-09
Progress Report: January 1,
2002—June 30, 2002
Erik D. Demaine
Project
Overview
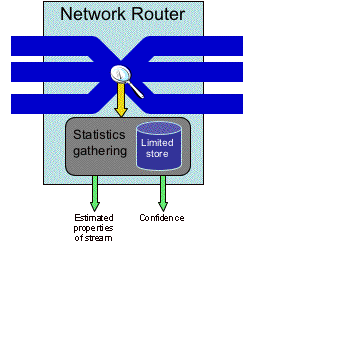 This project has developed algorithms and data
structures that extract essential characteristics of network traffic streams
passing through routers, namely the most common destination address, subject to
a limited amount of memory about previously seen packets. Such characteristics are essential for
designing accurate models and developing a general understanding of Internet
traffic patterns, which are critical for such applications as efficient network
routing, caching, prefetching, information delivery, and network upgrades.
This project has developed algorithms and data
structures that extract essential characteristics of network traffic streams
passing through routers, namely the most common destination address, subject to
a limited amount of memory about previously seen packets. Such characteristics are essential for
designing accurate models and developing a general understanding of Internet
traffic patterns, which are critical for such applications as efficient network
routing, caching, prefetching, information delivery, and network upgrades.
As
described in the previous progress report, we have designed and analyzed efficient
algorithms and data structures that have provable guarantees on the quality of
gathered statistics based on weak assumptions on the traffic distribution. We have considered the range from
deterministic, fully guaranteed algorithms (which are difficult but
surprisingly possible) to randomized, probabilistically guaranteed algorithms
(which are more powerful and achieve better bounds). On the other hand, we proposed to prove lower bounds on the
possible success of any algorithm.
This work is an ongoing collaboration with Prof. Alejandro López-Ortiz
and Prof. Ian Munro of the University of Waterloo.
Progress
Through June 2002
Since
the last progress report, we have concentrated on detailing and writing our
results in a paper, called “Frequency Estimation of Internet Packet Streams
with Limited Space.” This paper
includes several new results in terms of algorithms, data structures, and lower
bounds that are stronger than the results claimed before. We consider the general problem in
which packets are categorized
according to destination address, source address, etc., and the goal is to
identify the categories that
occur most frequently. The new
results can be summarized as follows:
1)
In the worst-case
omniscient-adversary model (where the network traffic distribution is
completely unknown):
a)
All categories that
occur more than 1/(m+1) of
the time, where m is the
number of counters that can be stored in memory, can (in particular) be
deterministically reported after a single pass through the stream. However, it is unknown which reported
categories have this frequency.
b)
This result is best
possible: if the most common category has frequency of less than 1/(m+1), then the algorithm can be forced to report
only uniquely occurring elements.
2)
In the stochastic
model (where the network traffic distribution is arbitrary but uniformly
permuted over time):
a)
All categories that
occur with relative frequency more than (c ln n)/sqrt(m n)
for a constant c > 0 can
be reported after a single pass through the stream, where n is the number of packets in the stream. Thus, as the stream gets longer, the
results get significantly better.
b)
The algorithm
estimates the frequencies of the reported categories to within a desired error
factor ε > 0 (influencing $c$).
c)
The results hold with
(polynomially) high probability,
meaning that the probability of failure is at most 1/nk for a desired constant k (also influencing c).
d)
This result is best
possible up to constant factors: if the maximum frequency is below f/sqrt(n m), then the
algorithm can be forced to report only uniquely occurring elements with
probability at least (e-1+1/e)f.
3)
Both of these
one-pass algorithms can be implemented by efficient data structures to use a
small constant amount of worst-case time per packet.
This
paper will be presented at the 10th Annual European Symposium on Algorithms, and will appear in the proceedings of the
conference, to be published in Springer-Verlag’s Lecture Notes in Computer
Science series. The paper is available at http://theory.lcs.mit.edu/~edemaine/papers/NetworkStats_ESA2002/. We have also prepared a full version of
the paper, which includes all details of algorithms and proofs, some of which
did not fit in the conference paper above. This version is a technical report at MIT and will be
submitted soon to a journal. It
too can be downloaded from the web, at http://theory.lcs.mit.edu/~edemaine/papers/NetworkStats_TR2002/.
We
have also begun exploring sources for real-world data to test our algorithms
experimentally on actual Internet traffic. In particular, we have initiated discussions with Mary Ann
Ladd, Technical Manager for the Computer Resource Services group at the MIT Lab
for Computer Science. The current
proposal is to gather packet headers that pass through the router connecting the
MIT Lab for Computer Science to the rest of the Internet, over the course of a
day or more. We have identified
the NetFlow system as a candidate approach to collecting this packet data from
Cisco routers.
Research
Plan for the Next Six Months
As
described above, our current plan is to implement the algorithms and test them
on real-world data. The first step
in this regard, currently in progress, is to gather the packet-header data of
actual network traffic. Then we
plan to implement the algorithms and run them in an offline manner on this data. By comparing their estimated statistics
with the perfect statistics (which we can compute exactly in this offline
scenario), we will evaluate both the practical relevance of our traffic
distribution assumptions, as well as how the parameters and worst-case analysis
affect the performance in practice.
Our expectations are that our algorithms will handle the true traffic
distribution effectively. We will
then see how much space is required to achieve low error rates, and consider
the practicality of having this much space in a physical router (the online
scenario). Our expectation from
our probabilistic analysis is that little space will be required.
We
will also continue to explore the theoretical side, which offers a range of
problems relating to network traffic monitoring. In the context of finding the most frequently occurring
elements, the most prominent problem is to determine to what extent
randomization and an oblivious adversary can allow us to improve the bounds even for the worst case. We are working on adapting a similar
algorithm to our stochastic algorithm by randomly perturbing the sizes of the
rounds. The idea is that such
perturbations prevent the adversary from knowing when the actual samples
occur. The probabilistic analysis
of this variant is significantly more complicated, and it remains to be seen
how good a bound can be achieved.
We are hopeful that a random perturbation strategy will lead to
interesting results in this context.