Model Reduction for Human and Animal Locomotion

MIT2001-08

Progress Report: July 1, 2002ãDecember 31, 2002

Jovan Popovic

Project Overview

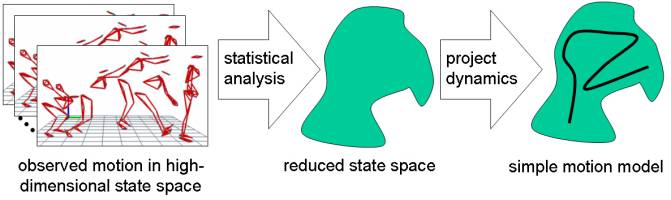Complexity of existing mathematical models inhibits the analysis and the automatic animation of human and animal motion. Current techniques rely on numerical simulations of highly nonlinear differential equations in high-dimensional spaces. A motion with such large-scale dynamics is difficult to control because of the sheer size of its control space. We are developing a method for constructing simpler mathematical models of lower dimensionality. The simplification consists of two steps: state-space reduction and model projection. The state-space reduction relies on statistical analysis of real-world observations to reduce the dimensionality of the original state space. The model projection constructs a new mathematical model on the reduced subspace by projecting the original equations of motion. The simplification will enable automated animation of complex mechanical systems.

Progress Through December 2002

Transformation of recorded human motion is an important application of our model reduction technique. The transformation techniques aim to produce a motion that complies with novel constraints while retaining the detail and style of the originally recorded motion. For example, if we record a human broad jump, we might want to elongate or shorten the jump without loosing the style of the original motion. This transformation problem can be stated as a constrained optimization with an objective function that minimizes the difference between recorded and transformed motion and constraints that make the resulting motion physical and that describe the requirements for new motion. Because large-scale dynamics of skeletal motion prevent robust convergence of this optimization in the high-dimensional state space, simple mathematical models produced by our model reduction approach are necessary.

In the last six months, we completed an implementation of the motion transformation technique that uses model reduction to approximate the dynamics of human motion. Our technique consists of three steps, which fit, transform and project recorded motion. The first step approximates recorded motion with a reduced model of human dynamics. We derive a separate reduced model for each human activity such as a walk, a broad jump, or a run. The derivation is a two-step process, which uses principal component analysis of motions within each class to reveal a low dimensional state space and Euler-Lagrange equations to evolve the dynamics of human motion on the reduced state space. The model describes the motion of the skeleton in response to the action of the internal skeleton forces. The fitting step infers the parameters that describe these forces with an optimization that maximizes the fit to recorded motion. This solution serves as a good initial guess for the transformation step, which adapts the recorded motion to comply with new animation requirements: for example, to extend or shorten a broad jump.

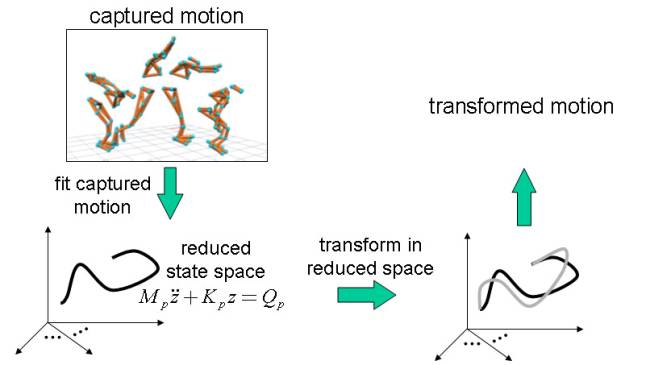
Figure 1. The motion transformation technique approximates recorded motion with a reduced model, transforms the motion in the reduced state space, and projects the transformed motion into the original high-dimensional state space.

The transformation step solves another optimization step to generate desired motion. Because the reduced model and the reduced state space encapsulate appropriate dynamics, the resulting motion remains physically consistent even as it complies with requested modifications. The last step completes the transformation by projecting the motion into its original high-dimensional space.

Research Plan for the Next Six Months

Although our current implementation generates reasonable motions for minor modifications of recorded motion, it does not generate visually pleasing results in most scenarios. We have several explanations for these problems:

∑ The current dynamics equations describe the motion of a human skeleton with a system of lumped-mass particles. This idealized approach may be an inadequate approximation of the true skeleton dynamics.

∑ The reduced model summarizes the action of human muscles with simple damped-spring forces. Although the stiffness and damping coefficients of these forces have intuitive meaning in the joint angle state space, their meaning is unclear in the reduced state space inferred by the principal component analysis.

In the next six months, we will determine the true causes of observed problems and devise appropriate solutions. The following table summarizes our work plan:

Time period	Task
January-February	Use linked rigid-body dynamics to transform low-dimensional motions without the reduced model of dynamics.
March	Compare the transformation with lumped-mass dynamics and the transformation with linked rigid-body dynamics.
April	Revise lumped-mass implementation and combine with model reduction
May	Revise linked rigid-body implementation and combine with model reduction
June	Evaluate lumped-mass and linked rigid-body implementations on motions of entire human skeletons.