Massachusetts Institute of Technology
Department of Electrical Engineering and Computer
Science
6.863J/9.611J Natural Language Processing, Spring,
2004
Laboratory 3, Components I and II:
Context-free parsing, Spring Warmup
Handed Out: March 10 Due: March 19
1. Introduction: Goals of the Laboratory & Background Reading
The main aim of this
laboratory is to give you a brief exposure to building “real” grammars, along
with an understanding of how syntactic phenomena interact with context-free
parsing algorithms. The laboratory is designed so that you will become familiar
with chart context-free parsing and the Earley parser we have described and
implemented, and the ways in which they achieve their efficiency, including the
important issue of how they deal with ambiguity. You will also examine in
detail one other parsing method, shift-reduce (bottom-up) parsing, as a way in
which to think about human parsing strategies.
We shall use this laboratory as a way of introducing you to the
terminology of linguistics and the way that we will describe more sophisticated
grammars that can handle cases of apparent ‘long distance’ dependencies, such
as the connection between ‘what’ and the object of the verb ‘eat’ in a sentence
such as ‘What did John eat?’ Finally,
you will learn how to use features-for example, those returned by the Kimmo or
part of speech taggers of Lab 2 – to simplify grammar construction, and
illustrate the important principle of modularity in NLP design- in this case,
the separation of lexical information from hierarchical, syntactic information.
The organization of this
laboratory is much like that of Lab 1.
Specifically, in the first part of the laboratory, Component II, we will
introduce you to the subject and give you some ‘warmup’ questions to think
about parsing, as well as introduce you to running the shift-reduce, chart, and
Earley parsers. A few of the questions may require more than casual thinking.
In the second part of the lab handed out next time, Component III, you will
have the job of implementing a larger grammar to capture certain syntactic
phenomena in English.
General
Background reading for this Laboratory
You should prepare for this laboratory by reading the following: First, the third and fourth installments of course notes on the website here and here provide an overview of syntactic structure and parsing, including much more detail on Earley parsing than we can provide in this document. Second, we include below concise descriptions of general context-free parsing, shift-reduce parsing, and chart parsing. Finally, your textbook’s chapters on context-free parsing offer additional discussion of chart parsing and the general topic of context-free parsing.
Running the
parsers
The material in the subsequent sections describes in detail how to use and run the parsers for the laboratory. A concise reference summary of the operation of the first two can be obtained by selecting the “Help” button in each.
(Note: much of the following material is taken, slightly modified, from
Edward Loper and Steven Bird’s introduction to these parsers)
1.1
Why parsing?
Native speakers of any language have strong intuitions about the well-formedness of sentences in that language. These intuitions are surprisingly detailed. For example, consider the following six sentences involving three synonymous verbs loaded, dumped, and filled. (We shall return to this question later in the course, under the heading of lexical semantics.)
a. The farmer loaded sand into the cart
b. The farmer loaded the cart with sand
c. The farmer dumped sand into the cart
d. *The farmer dumped the cart with sand
e. *The farmer filled sand into the cart
f.
The farmer filled
the cart with sand
g. I wonder who likes ice-cream
h. *What do you wonder who likes
Three of the sentences (starred) are ill-formed.
As we shall see, many patterns of well-formedness and ill-formedness in a
sequence of words can be understood with respect to the internal phrase
structure of the sentences. We can develop formal models of these
structures using grammars and parsers. In particular, as we have discussed, we
can use context-free grammars to describe the phrase structure – at least for
part of natural languages.
In the context of computational modeling, a
language is often viewed as a set of well-formed sentences. Sequences of words
that are not grammatical are excluded from this set. We remind you again that this notion of
‘grammatical’ is one that may have little in common with prescriptive
grammar that you might have been taught in elementary school. Now, since there
is no upper-bound on the length of a sentence, the number of possible sentences
is unbounded. For example, it is possible to add an unlimited amount of
material to a sentence by using and or by chaining relative clauses,
as illustrated in the following example from a children's story:
You can
imagine Piglet's joy when at last the ship came in sight of him. In after-years
he liked to think that he had been in Very Great Danger during the Terrible
Flood, but the only danger he had really been in was the last half-hour of his
imprisonment, when Owl, who had just flown up, sat on a branch of his tree to
comfort him, and told him a very long story about an aunt who had once laid a
seagull's egg by mistake, and the story went on and on, rather like this
sentence, until Piglet who was listening out of his window without much hope,
went to sleep quietly and naturally, slipping slowly out of the window towards
the water until he was only hanging on by his toes, at which moment, luckily, a
sudden loud squawk from Owl, which was really part of the story, being what his
aunt said, woke the Piglet up and just gave him time to jerk himself back into
safety and say, "How interesting, and did she?" when -- well, you can
imagine his joy when at last he saw the good ship, Brain of Pooh (Captain, C. Robin;
Ist Mate, P. Bear) coming over the sea to rescue him... (from A.A. Milne In
which Piglet is Entirely Surrounded by Water)
Given that the resources of a computer, however
large, are still finite, it is necessary to devise a finite description of this
infinite set. Such descriptions are called grammars. We have already
encountered this possibility in the context of regular expressions. For
example, the expression a+ describes the infinite set {a, aa,
aaa, aaaa, ...}. Apart from their compactness, grammars usually capture
important properties of the language being studied, and can be used to
systematically map between sequences of words and abstract representations of
their meaning. Thus, even if we were to impose an upper bound on sentence
length to ensure the language was finite, we would still want to come up with a
compact representation in the form of a grammar.
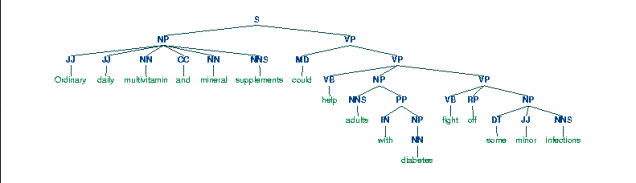
A well-formed sentence of a language is more than an arbitrary sequence of words from the language. Certain kinds of words usually go together. For instance, determiners like the are typically followed by adjectives or nouns, but not by verbs. Groups of words form intermediate structures called phrases or constituents. These constituents can be identified using standard syntactic tests, such as substitution. For example, if a sequence of words can be replaced with a pronoun, then that sequence is likely to be a constituent. The following example illustrates this test:
a. Ordinary daily multivitamin and mineral supplements could help adults with diabetes fight off some minor
infections
b. They could help
adults with diabetes fight off some minor infections
What these tests do is something like figuring out
what an element is in chemistry: if two items A and B act alike under
similar syntactic operations, then they are in the same equivalence class. You may recall that the notion of ‘act alike’ with morphology had to do with
linear strings of characters. Here the notion is more sophisticated, and relies
on hierarchical structure, as discussed in the notes and the class
lectures.
The structure of a sentence may be represented
using a phrase structure tree, in which the terminal symbols are the words of
the sentence, the pre-terminal symbols are parts of speech, and the remaining
non-terminals are syntactic constituents. An example of such a tree is shown in
Figure 1. Note that we use the Penn Treebank POS tags
here as the symbols that immediately dominate the actual word tokens (the
‘fringe’) of the tree. Such POS symbols
are usually called preterminals, because the actual fringe elements of a
tree like the words are called terminals. Recall that a phrase structure tree is a representation of all
the dominance and precedence relations that would be obtained in a derivation
of the fringe of the tree from the Start, or S node.
Figure 1. Phrase Structure Tree
A grammar is a formal system that
specifies which sequences of words are well-formed in the language, and which provides
one or more phrase structures for the sequence. We will focus our attention on
a particular kind of grammar called a context-free grammar (CFG),
which is a collection of productions of the form S → NP VP.
(To be well-formed, each non-terminal node and its children must correspond to
such a production.)
A parser is a computational system that
processes input sentences according to the productions of the grammar, and
builds one or more constituent structures which conform to the grammar. We take
a grammar to be a declarative specification of well-formedness, and a parser to
be a procedural interpretation of the grammar. Here we will present
context-free grammars, and describe some simple parsers that work with them.
Parsing is important in linguistics and natural
language processing for a variety of reasons. A parser permits a grammar to be
evaluated against a potentially large collection of test sentences, helping the
linguist to identify shortcomings in their analysis. A parser can be used as a
model of psycholinguistic processing, and used to explain the processing
difficulties that humans have with certain syntactic constructions (e.g. the
so-called ``garden path’’ sentences). A parser can serve as the first stage of
processing natural language input for a question-answering system, as a
pipeline for semantic processing (again, we will treat this in a later
laboratory).
2. Computational Approaches to Parsing: Description and Laboratory Questions
You should refer to the online notes and lectures for much more detailed
background on the following material.
In the following three subsections (2.1, 2.2, 2.3, and 2.4) we shall
take a look at four distinct parsing methods: recursive-descent parsing; shift-reduce
parsing; chart parsing; and Earley parsing.
Questions will pertain only to the last three.
2.1. Recursive Descent
Parsing: Top-down, depth-first search
The simplest kind of parser interprets the grammar
as a specification of how to break a high-level goal into several lower-level
subgoals. The top-level goal is to find an S. The S → NP
VP production permits the parser to replace this goal with two subgoals:
find an NP, then find a VP. Each of these subgoals can be
replaced in turn by sub-sub-goals, using productions that have NP
and VP on their left-hand side. Eventually, this expansion process
leads to subgoals such as: find the word telescope. Such subgoals
can be directly compared against the input string, and succeed if the next word
is matched. If there is no match the parser must back up and try a different
alternative.
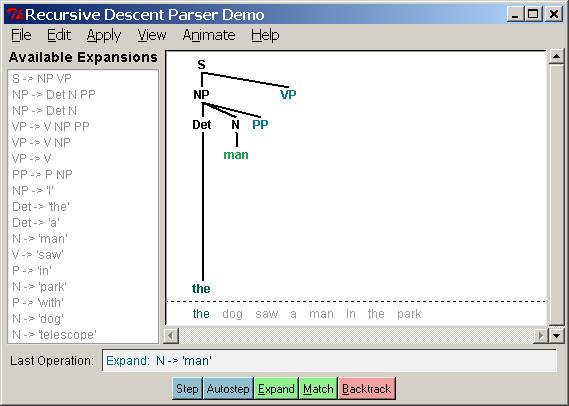
The recursive descent parser builds a parse tree
during the above process. With the initial goal (find an S), the S
root node is created. As the above process recursively expands its goals using
the productions of the grammar, the parse tree is extended downwards (hence the
name recursive descent). Let’s
see how it works. We do not ask any questions or ask you to run
this parser in the laboratory – we simply want you to study the execution
pattern.
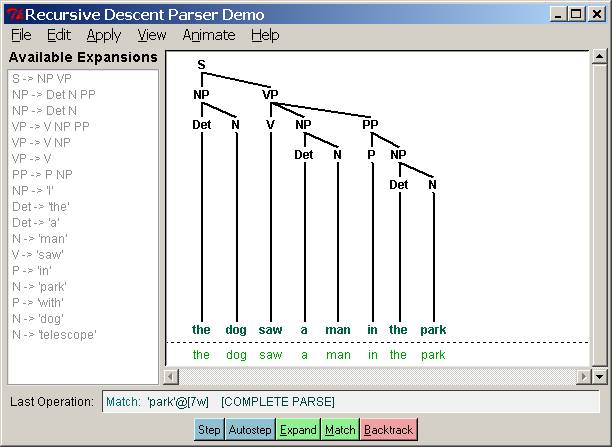
Several stages of the execution of this parser are
shown in Figure 2.
Figure 2. Several stages
of a Recursive Descent Parser: initial, after failing to match “man,” completed
parse.
Recursive descent parsing: considers structures
and words that are not in the input. Further, backtracking may discard parsed
constituents that need to be rebuilt; for example, backtracking over VP
→ V NP will discard the structures created for the V and
NP non-terminals. If the parser then proceeds with VP → V
NP PP, then the structures for the V and NP must be
created again. This is inefficient –
it violates principle AWP. As we
discussed in class, and as in the notes, by adding the notion of a chart
we can remove this inefficiency, essentially by dynamic programming, of the
kind you are familiar with from 6.034 A* search.
Recursive descent parsing is a kind of top-down
parsing. These use the grammar to predict what the input will be,
before inspecting any input. However, since the input is available to the
parser all along, it would be more sensible to consider the input sentence from
the very beginning. Such an approach is called bottom-up parsing.
2.2. Shift-Reduce Parsing: Bottom-up search
The simplest kind of bottom-up parsing is known as
shift-reduce parsing. The parser repeatedly pushes the next input
word onto a stack; this is the shift operation. If the top n
items on the stack match the n items on the right-hand side of some production,
then they are all popped off the stack, and the item on the left-hand side of
the production is pushed on the stack. This replacement of the top n
items with a single item is the reduce operation. The parser finishes
when all the input is consumed and there is only one item remaining on the
stack, a parse tree with an S node as its root. There are thus only two
operations that this parser ever uses: shift and reduce.
|
|
Note that the reduce operation may only be applied to the top of the stack. Reducing items lower in the stack must be done before later items are pushed onto the stack. |
The shift-reduce parser builds a parse tree during
the above process. If the top of stack holds the word dog and if the
grammar has a production N → dog then the reduce operation
causes the word to be replaced with the parse tree for this production. For
convenience we will represent this tree as N(dog). At a later stage,
if the top of the stack holds two items Det(the) N(dog) and if the
grammar has a production NP → Det N then the reduce operation
causes these two items to be replaced with NP(Det(the), N(dog)).
This process continues until a parse tree for the entire sentence has been
constructed. Importantly, such a parser
is nondeterministic: with some grammars and sentences, it must choose
between equally applicable shift or reduce actions, and can make a mistake: if
it chooses to reduce two elements on the stack, instead of shifting
a new word on the stack, then it may finish a phrase too soon. Or the opposite
could happen: it could shift an element on the stack, when it should have
reduced the current stack. This is
called a shift/reduce conflict.
Let us see this parser in action – this will be
the first computational and question part of the Lab. Login to Athena and do: add 6.863 as usual. To
run the shift-reduce parser, dubbed srparser, you simply have to invoke
it at the command line. It will already
be primed with the example sentence and grammar that we need for questions,
that we show below – we won’t be loading any grammar or lexicon files for this
demo.
athena% srparser
This should pop up a window like the following. To the right is the stack and the remaining
input. To the left is the entire
grammar. Please take a moment to examine
it. You should at this point click the “Help” button and read about the basic
operation of the parser and what all the menu buttons do. (However, please don’t fiddle with grammar
or text editing at this point.) To run the parser, just click the button at the
bottom labeled ‘Step’. That will
execute one step, either shift or reduce, with animation. The default is set
for a reasonable animation speed that you may change via the Animate item at
the top menu bar. Note again that the
parser has only two operations it can use: (1) Shift an item (a
word) onto the stack; or (2) Reduce items on the stack into a single
symbol. Which one it has just carried
out is given by the information at the lower left, in “Last Operation”
panel. If you continue to click “Step,”
the parser will keep applying actions until it either reaches a complete parse,
with only S and a tree structure beneath S left on the stack and nothing in the
remaining text, or else get stuck.
· Please try this now, with the sentence
the parser initially starts with, “my dog saw a man in the park with a
statue.” If you get stuck at any
point, you can just go to the File menu and reset the parser to the same
grammar and input sentence.
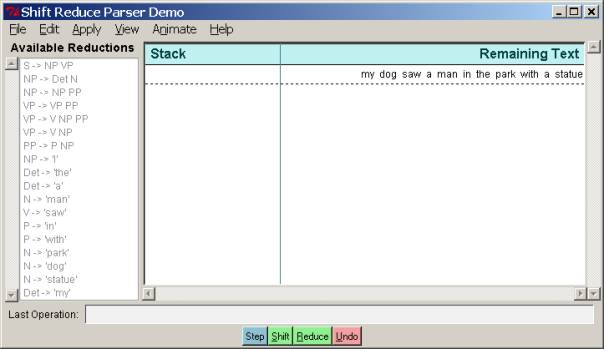
In the rest of this section we will ask some simple questions
concerning the operation of srparser.
Note that you can take snapshots of the parser’s stack and input via the
File menu item “Print to postscript”, also Ctl-P. (You will have to save the .ps file to your
own directory). You can then view this
with a postscript tool, e.g., ghostscript <name of
postscript file>. You may have
to invoke the command add
gnu to make sure that ghostview is available. OK, on to some questions.
Question 1. Shift-reduce parsing.
Please take a snapshot of exactly where the parser gets stuck on
this sentence – that is, the state of the stack and input when it can make no
further moves -and include it in your lab report. This dead-end was caused by the parser’s incorrect choice between
a shift and a reduce action. This is called a shift-reduce
conflict.
To get around this parsing mis-step, you can now back up the parser by repeatedly hitting the
“Undo” button. Do that now, and
determine at what point in the parser’s choice between shift and reduce
actions the actual incorrect choice was made. By “at what
point” we mean literally the number of times you had to click the “Step” button
to arrive at the incorrect shift/reduce decision point. Please make a snapshot
of that point to include in your report and describe what the mistake was,
e.g., “the parser did X when it should have done Y”.
You can now proceed with the parse by correcting the wrong choice
- by pressing the “Shift” or “Reduce” button yourself before the bad decision
is made, as appropriate. Do that, and,
now that this wrong choice has been corrected, run the parser forward again
automatically by hitting the “Step” button repeatedly. Please show where the parser gets stuck now,
and again describe why – which shift/reduce choice, possibly earlier in the
parse, was responsible, and at what Step number this occurred.
In all then, your answer to Question 1 should include three
snapshots, and two brief characterizations of the parser errors.
Question 2. Parsing
Strategies. We see
therefore that parsers must in general operate ‘nondeterministically’ – that
is, they must guess. This is the source of computational difficulty in natural
language processing. Since no physical machine can operate
nondeterministically, we must somehow either dodge this problem, or else
simulate a nondeterministic machine. Below, in the next section, we shall see
how to do nondeterministic simulation.
Here however, we shall pursue another possibility: developing a way to
‘always make the right choice’ – that is, a parsing strategy that orders
choices systematically when more than one action can apply at a given
step. In a shift-reduce parser, there
are only two possible such conflicts: (1) a shift-reduce conflict (should the
parser shift a word onto the stack or instead reduce items on the stack into a
new nonterminal); or (2) a reduce-reduce conflict, if there is more than one
way to reduce the nonterminals on the stack into a single new nonterminal. A strategy is a systematic
resolution of these conflicts, imposed on the parser’s actions. For example, we
could decide to always resolve shift-reduce conflicts in favor of shift
actions: if a conflict occurs, always shift an item onto the stack, and do not
reduce. Or, we could decide to do the
opposite. We can denote these two
strategies as follows: shift >
reduce means that shift takes precedence over reduce, whenever a conflict
occurs, whereas reduce > shift means the opposite.
Question 2(a): Looking over your answer to Question1, how would you
best characterize the strategy that the parser is automatically using? Is it shift
> reduce or reduce > shift?
Justify your answer.
Question 2(b): Can you select a single strategy that will work for
the example sentence in Question 1 – that is, will be able to go through the
entire sentence and produce a parse? (Please ignore the way in
which the parser puts together NP and VP to form an S – let us just say that
this decision is postponed until the very end.) Justify your answer.
Question 2(c): The choice
of strategy will also affect the shape of the resulting parse
trees – that is, whether they are ‘bushy’ – flatter rather than deeper – or
‘straggly’ – branching down to the right or left. Please characterize the parse
tree shapes that each strategy will produce, in these descriptive terms, and
justify by providing examples using our example sentence, of parse trees that
exhibit these properties.
Question 2(d): Which strategy has the effect of minimizing the
number of elements on the stack (the stack ‘depth’)? Why? We might think of
this as ‘memory load’, so this has had an influence on studies of how people
process sentences, since people have very little stack memory, it seems.
Question 2(e): Putting to one side for the moment issues about
‘meaning’, people seem to have definite preferences in the way that they
construct parse trees for sentences such as, “my dog saw a man in the park with
a statue on the grass behind the fence.”
Does this preference seem to follow shift > reduce, reduce >
shift, or neither? Please explain.
Question 3. Reduce-reduce conflicts. In a reduce-reduce conflict, the parser will
have two or more competing rules to reduce the elements in the stack to a
single nonterminal, e.g., taking an NP and PP on the stack and reducing it to
an NP would conflict with another rule that would reduce an NP and a PP.
Question 3(a): Are there any reduce-reduce conflicts in the srparser
grammar? If so, produce a snapshot
showing the state of the stack and input illustrating the possibility. If not, explain why, given the particular
grammar here, that this cannot occur.
Question 3(b): Propose a stategy resolution to reduce-reduce
conflicts and explain why it is a reasonable one. (Don’t try too hard – just
come up with something sensible.)
Question 4. Stack depth and Time Complexity. Sentences
as in Question 3, “My dog saw a man in the park…” can of course grow in length
without bound. Let us write them, using a shorthand for PP and NP, as follows:
NP V(erb) NP PP PP PP… As we saw in
class, the number of possible parses for such sentences grows roughly
proportional to the terms in a Fibonacci series, and so, beyond polynomial:
there for NP V NP PP there are two
possible parses – the PP can modify the NP after the verb, or the verb (in our
grammar this is done by the rule VP ®VP
NP). For V NP PP PP, there are five – the last PP can modify the second PP, the
NP, or the VP, and then there are the two parses from the previous V NP PP. And
so on. Since we are ignoring meaning, we could of course just write out such
sentences as, “saw a guy in the park in the park in the park….” In this
question we look at how bad this can get, since this is the worst case for
parsing – we call it ‘arbitrary ambiguity.’
Question 4(a): We measure
such sentences in terms of n, their length in number of words (or parts
of speech, really, like N or V). As n
grows without bound, how deep can the stack of the shift-reduce parser grow, in
terms of n?. We want you to
provide an order estimate – that is, some form using the order notation O(
…) that is an asymptotic upper bound. Explain your answer. If you are
unfamiliar with this notation, you can read about it via the Wikpedia
definition here. (We assume that if a sentence cannot be
parsed then its parsing time doesn’t count in this calculation.)
Question 4(b). We say that a parsing computation is linear time if its time complexity is O(n) where n is the input sentence length. In other words, there is some constant k s.t. the time is bounded asymptotically from above by kn. We say that a parsing computation is real time if its computation is exactly equal to time n. That is a stronger claim, with k=1. Conventionally, this means that a real-time computation cannot take more than a fixed, finite number of steps before it must process an input symbol. In our case, this would mean a fixed number of steps before a symbol had to be shifted onto the stack. To see that this is a stronger constraint than linear time, note that a computation could be linear time but not real-time: if a computation is not real time, there could be an arbitrarily long pause, proportional, for example, to kn, before the next input symbol would be processed. Such a computation would still be linear time – proportional to kn – but not real-time. (Here is the classic reference: A. Rosenberg, “Real-time definable languages,” Journal of the Association for Computing Machinery, Volume 14 , Issue 4 (October 1967), 645 – 662.)
One might argue that human sentence processing must be real-time in the sense that when we ‘process’ input words there never is a possibly arbitrarily long pause that depends on the length of the sentence before we process the next word (What never? Well, hardly ever…it’s arguable in the case of certain individuals who shall go nameless here.) Let’s assume that.
If so, is the srparser real-time? If it is, explain why. If
not, explain why not and give an example sentence that would force the parser
to violate the real-time constraint. (Look at the previous questions for
insight.) This bears on whether the srparser
really could serve as a model of human sentence processing or not.
Bonus challenge question. [For algorithm enthusiasts only – completely
optional, but indeed a bonus]. We
remarked above that the number of parses in a sentence like Verb NP PP PP…
grows like a Fibonacci series. That’s
not quite accurate. Close, but no cigar.
In fact, the number of parses is identical to the number of ways to
parenthesize (partition) a string of n symbols. For example, the string xxx can be
parenthesized as (x (xx)), (xxx), ((xx)x), e.g., ((Verb NP) PP), (Verb (NP PP)), (Verb NP PP). Find a recurrence relation that
characterizes the growth of this number.
If you are really ambitious (and haven’t swiped the answer from Knuth),
try to solve the recurrence (you will need Stirling’s formula to approximate
factorial growth. Some hint, huh?)
2.3 Chart Parsing: Dynamic
programming for parsing – the Avoid Work Principle & generalized search
The bottom-up shift-reduce parser can only find one parse, and it often fails to find a parse even if one exits. The top-down recursive-descent parser can be very inefficient, since it often builds and discards the same sub-structure many times over; and if the grammar contains left-recursive rules, it can enter into an infinite loop.
These completeness and efficiency problems can be addressed by employing a technique called dynamic programming, which stores intermediate results, and re-uses them when appropriate. Or, you can look at it like the idea of memorizing a function, which you might remember from 6.001. The end result will be a method called chart parsing. What follows is a description of that method, followed by several snapshots working through our running implementation of this method. Be advised: it is a loooong way to the next Question, question 5 – but you should review the material, if only to see how to run the chart parser.
In general, a parser hypothesizes constituents based on the grammar and on the current state of its knowledge about the tokens it has seen, and the constituents it has already found. Any given constituent may be proposed during the search of a blind alley; there is no way of knowing at the time whether the constituent will be used in any of the final parses which are reported. Locally, what we know about a constituent is the context-free rule (production) that licenses its node and immediate daughter nodes (i.e. the "local tree"). Also, in the case of chart parsing, we know the whole subtree of this node, how it connects to the tokens of the sentence being parsed, and its span within the sentence (i.e. location). In a chart parser, these three things: rule, subtree and location, are stored in a special structure called an edge.
Consider a sequence of word tokens, e.g. the park. The space character between the two tokens is a shared boundary. There are further token boundaries at the start and end of the sequence. We can make these boundaries explicit like this: • the • park • . Now think of these bullets as nodes in a graph. Each word can be thought of as an edge connecting two nodes. Since each of these edges corresponds to exactly one token, we call them token edges. These are the simplest type of edge. However, we can generalize the notion of an edge to edges that span more than one token. Consider again our words and boundary markers: • the • park • . In addition to the two token edges, we can have a third edge which connects the initial and final boundaries, spanning two tokens. This edge could represent a noun phrase constituent. We call these production edges.
A chart is a collection of edges, each representing a token or a hypothesis about a syntactic constituent. A chart parser explores the search space that is licensed by the grammar and constrained by the input sentence, all the time inserting additional edges into the chart. The chart parsing strategy (e.g. top down or bottom up) controls the way in which the parser operates with its three sources of information: the grammar, the input sentence, and the chart. In fact, we describe all possible search strategies using a chart – there are intermediates between top-down and bottom up, such as Earley parsing, which is described in the next section.
The purpose of an edge is to store a particular hypothesis about the syntactic structure of the sentence. Such hypotheses may be either complete or partial. In a complete edge, each terminal or non-terminal on the right-hand side of the production has been satisfied; supporting evidence for each one exists in the chart. The above example contains a complete edge, represented as [-----] or [=====] (the latter is for complete edges that span the entire chart). The right-hand side of its production consists of two terminals, and for each of them there is a corresponding edge in the chart. This is the format that the log files for our parser will use, that you may have to examine in answering some questions.
In a partial edge, the right-hand side of the production is not yet fully satisfied. An asterisk is used to indicate how much of the production has been satisfied. For example, in the partially matched production NP®- 'the' * 'park', only the material to the left of the asterisk, the word the, has been matched. The symbol immediately to the right of the asterisk is the next symbol (terminal or non-terminal) to be processed for this edge. For example:
|[--] .| 'the'.
|. [--]| 'park'.
|[--> .| NP -> 'the' * 'park'
The span of the edge, depicted as [--> only corresponds to the material that has been matched. The greater-than symbol indicates that the edge is incomplete. Note that an incomplete edge stores a complete tree corresponding to the production; this is the hypothesis it is attempting to verify. By convention we omit the final asterisk that appears at the very end of a complete edge, e.g., NP ® 'the' 'park' *.
The only remaining logical possibility is for the asterisk to be at the start, e.g. NP ® * 'the' 'park'. This is a special case of an incomplete edge having zero width (i.e. a self-loop which begins and ends at the same node). Zero-width edges represent the hypothesis that a syntactic constituent begins at this location, however no evidence for the right-hand side of the production has yet been found.
The set of edges at any particular position i in the chart, as we move from left (position 0) to right (the end of the sentence position) actually denotes the set of states the parser could be in after reading i words. Thus, what we are really doing is simulating a nondeterministic machine by computing the set of next states it could be in at any given step. The state description is the set of edges (the start and stop positions of an edge, along with its dotted rule label).
In the process of chart parsing, edges are combined with other edges to form new edges that are then added to the chart. Nothing is ever removed from the chart; nothing is modified once it entered in the chart.
2.3.1 Charts
A chart is little more than a set of edges. The edge set represents the state of a chart parser during processing, and new edges can be inserted into the set at any time. The chart also stores a location. This represents the combined span of the list of input tokens, and is supplied when the chart is initialized. The chart uses this information in order to identify those edges that span the entire sentence. When such an edge exists, and also has the required non-terminal, its associated tree is a parse tree for the sentence.
There are three ways in which edges are added to a chart during the parsing process: when the parser first encounters words; when it first encounters a nonterminal (phrase name); and when it glues together two edges to form a larger one.
1.
Add an initial edge for every word token. This is done as an initialization step.
2.
Given a context-free production rule and a chart,
create a zero-width edge at the specified location, and put an asterisk at the
start of the production's right-hand side. This is called a self-loop edge
because the start and stop location of the edge at that point happen to be
identical. For example, if we begin a
noun phrase (NP) at position 0 of the input, then the edge runs from 0 to 0,
labeled with an NP
3.
The third way of adding edges is more complicated.
It takes a pair of adjacent edges and creates a new edge spanning them both. It
only does this if: (i) the left edge is incomplete; (ii) the right edge is
complete; and (iii) the next symbol after the asterisk on the right-hand side
of the left edge's production matches the symbol on the left-hand side of the
right edge's production. This is called the fundamental rule,
which we return to below.
2.3.2 Chart Rules
A chart parser is controlled by a rule-invocation strategy, which determines the order in which edges are added to the chart. In this section we consider the various kinds of chart rules that make up these strategies. Each rule examines the productions in the grammar and the current edges in the chart, and adds more edges. All strategies begin by loading the tokens into the chart, creating an edge for every token (using the first edge-addition method described in the last section). This work is done when the chart parser is created.
There are four rules that we must describe: (1) the bottom-up rule; (2) the top-down initialization rule; (3) the top-down rule; and (4) the fundamental rule. Rules (1)-(3) introduce new edges into the chart, while only rule 4 glues previous edges together into new, longer ones.
Bottom
Up Rule
A bottom up parser builds syntactic structure starting from the words in the input. For each constituent constructed so far, it must consider which grammar rules could be applied. For each complete edge, it gets the symbol on the left-hand side of that edge's production, then finds all productions in the grammar where that symbol appears as the first symbol on the right. For example, if there is an existing complete edge with the production VP ® V NP then it identifies the left-hand side (VP) then searches for productions in the grammar of the form X ® VP .... All such productions are then inserted into the chart as zero-width edges. In Python code form (you don’t have to know Python to read this closely – you can get the gist from just glancing at it.) We could write the function BottomUpRule this way:
# For each complete edge: >>> for edge in chart.complete_edges():# For each production in the grammar:
... for production in grammar.productions():
# Does the edge LHS match the production RHS?
... if edge.lhs() == production.rhs()[0]:
... location = edge.location().start_location()
... chart.insert(self_loop_edge(production, location))
Now we consider the action of this rule in the context of a simple grammar. We initialize the chart with the tokens. For each token we, find a production in the grammar and add a zero-width edge. The grammar we use is like the very basic one from the srparser:
S
-> NP VP
NP -> Det N
NP -> NP PP
VP -> VP PP
VP -> V
PP -> P NP
Along with the lexicon rules (preterminal expansions):
NP -> I
N -> dog
N -> cookie
Det -> my
Det -> the
V -> saw
P -> with
If we now apply the initialization for words and the bottom-up edge creation rule to the sentence “I saw the dog with my cookie” we get the following, which is the actual log output that you will see from the chart parser. Each dot represents one input position - with an implicit dot at the front not shown at the front. Completed edges are given in square brackets. Thus we have the ‘word’ edges in square brackets showing that these are already completed. The bottom-up rule then produces seven new edges, corresponding to each of these lexical rules.
Lexical Insertion |[--] . . . . . .| 'I'.
Lexical Insertion |. [--] . . . . .| 'saw'.
Lexical Insertion |. . [--] . . . .| 'the'.
Lexical Insertion |. . . [--] . . .| 'dog'.
Lexical Insertion |. . . . [--] . .| 'with'.
Lexical Insertion |. . . . . [--] .| 'my'.
Lexical Insertion |. . . . . . [--]| 'cookie'.
Bottom Up Rule |. . . . . . > .| N -> * 'cookie'
Bottom Up Rule |. . . . . > . .| Det -> * 'my'
Bottom Up Rule |. . . . > . . .| P -> * 'with'
Bottom Up Rule |. . . > . . . .| N -> * 'dog'
Bottom Up Rule |. . > . . . . .| Det -> * 'the'
Bottom Up Rule |. > . . . . . .| V -> * 'saw'
Bottom Up Rule |> . . . . . . .| NP -> * 'I'
Observe that the new zero-width edges have productions with an initial asterisk. This is as far as the bottom-up rule can go without the help of the fundamental rule, discussed below.
Top
Down Initialization
Top down parsing is initialized by creating zero-width edges at the leftmost position in the chart. For every grammar rule whose left-hand side is the base category of the grammar, we create the corresponding dotted rule with the dot position at the start of the right-hand side.
# for each production in the grammar: >>> for production in grammar.productions(): # does the production expand the start-symbol of the grammar?
... if production.lhs() == grammar.start():
... loc = chart.location().start_location()
... chart.insert(self_loop_edge(production, location))
We can apply this rule to the above example. The start symbol of the grammar is S and there is only one production having S on its left-hand side, namely S ® NP VP. The top down initialization rule inserts a zero-width edge with this production, at the very left of the chart:
Lexical Insertion |[--] . . . . . .| 'I'.
Lexical Insertion |. [--] . . . . .| 'saw'.
Lexical Insertion |. . [--] . . . .| 'the'.
Lexical Insertion |. . . [--] . . .| 'dog'.
Lexical Insertion |. . . . [--] . .| 'with'.
Lexical Insertion |. . . . . [--] .| 'my'.
Lexical Insertion |. . . . . . [--]| 'cookie'.
Top Down Init Rule |> . . . . . . .| S -> * NP VP
Top
Down Rule
Whenever a chart contains an incomplete edge, with an incomplete rule having X as the next symbol (to the right of the asterisk), we know that the parser is expecting to find an X constituent immediately to the right. The top-down rule looks for all incomplete edges expecting an X and, for each production having X on its left-hand side, creates a zero-width edge containing this production on the right of the incomplete edge. This expresses the top-down prediction that the hypothesized constituent exists, and evidence for it should be sought immediately to the right. We could right the function TopDownRule this way:
# for each production in the grammar: >>> for production in grammar.productions(): # for each incomplete edge in the chart:
... for edge in chart.incomplete_edges():
# does the expected constituent match the production?
... if edge.next() == production.lhs():
... location = edge.location().end_location()
... chart.insert(self_loop_edge(production, location))
As before, we apply this rule to our running example:
Lexical Insertion |[--] . . . . . .| 'I'.
Lexical Insertion |. [--] . . . . .| 'saw'.
Lexical Insertion |. . [--] . . . .| 'the'.
Lexical Insertion |. . . [--] . . .| 'dog'.
Lexical Insertion |. . . . [--] . .| 'with'.
Lexical Insertion |. . . . . [--] .| 'my'.
Lexical Insertion |. . . . . . [--]| 'cookie'.
Top Down Init Rule |> . . . . . . .| S -> * NP VP
Top Down Rule |> . . . . . . .| NP -> * 'I'
Top Down Rule |> . . . . . . .| NP -> * Det N
Top Down Rule |> . . . . . . .| NP -> * NP PP
Top Down Rule |> . . . . . . .| Det -> * 'the'
Top Down Rule |> . . . . . . .| Det -> * 'my'
Fundamental Rule
In section 2.3.2 we encountered a rule that combines the information from two edges and creates a new edge. This method of combining edges is known as the Fundamental Rule. It is so important that we repeat the definition, using more formal notation. Suppose that an edge e1 has a dotted rule whose next symbol is X. Suppose that a second edge e2, immediately to the right of e1, represents a complete X constituent. Then the Fundamental Rule states that we must add a new edge e3 spanning both e1 and e2, in which the dot is moved one position to the right. In other words, e1 was looking for an X to its right, which it found on e2, and we record this fact on e3. This rule is applied as many times as possible – to all pairs of adjacent edges that match the above criteria. We can think of this rule as ‘pasting’ or concatenating two hierarchical structures into one larger one.
2.3.4 Chart Parser Strategies
Chart parsers use the various rules described above in order to emulate top down, bottom up or hybrid parsers. A policy about what chart rule should be applied under what circumstances is called a rule-invocation strategy. Here are the definitions of the two most common strategies, where we use abbreviations TopDownRule, BottomUpRule, and FundamentalRule for the descriptions we gave above. Note that there are other intermediate strategies, as we mentioned earlier.
>>> TD_STRATEGY = [TopDownRule(), FundamentalRule(), TopDownInitRule()] >>> BU_STRATEGY = [BottomUpRule(), FundamentalRule()]
A chart parser is initialized with a parsing strategy. During the parsing process, it repeatedly applies the rules of the strategy until no new edges are added. It may seem strange that we have created complex chart parsing machinery only to redefine the top-down and bottom-up parsers. However, these versions are much more efficient, since they cache intermediate parse results in the chart. In fact, it can be shown that the chart is sufficient for these methods to achieve polynomial time parsing complexity.
2.4. Chart Parsers
Given these complete strategies, we can now parse the input sentence and generate parse trees. The parser finds two trees, owing to the syntactic ambiguity in the prepositional phrase attachment. Let’s see how this works by actually running the parser. Again, once you have added 6.863 at the Athena prompt, you can invoke the chart parser with a demo grammar and a demo sentence (not the sentence below), via the following:
athena% chart
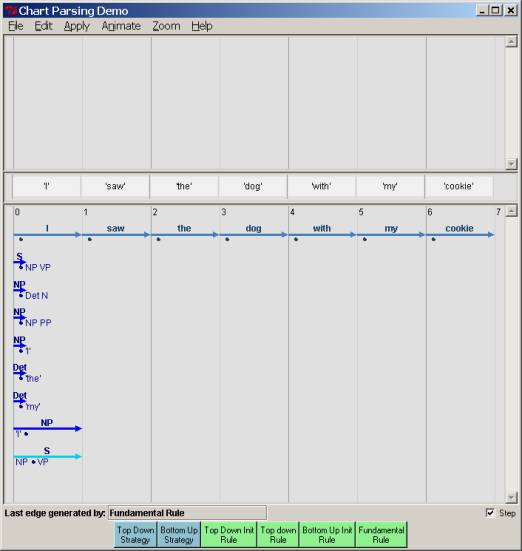
This will pull up the following interface as shown below. Click on the ‘Help’ menu item to get a more complete description if you want. At the middle you see the sentence to be processed, with the (now empty) chart below. At the bottom you now see that we have the four rules we talked about, in green, along with the two possible strategies, bottom-up and top-down, in blue To run a top-down parse, you click on the “top-down init” button first, and then the “Top-down strategy” button. Then the parse will then run automatically at a speed specified in the “Animation” menu selection, adding edges until it can no longer do so, using the rules as we described. You will see the parsing edges introduced into the chart as they are produced, in light blue. If there is a correct parse, the chart parser will output more than one: You will see that there is a correct parse if there is one (or more) edges running all the way from point 0 to the end of the sentence, labeled S. Clicking on any complete S edge will show its parse tree, above the word line. Below, we show the state of the chart just after clicking the “Top down Init Rule”. Note that the Rule S®· NP VP has been placed in position 0 in the chart, as described earlier. The dot is before a nonterminal, S, so this ought to prompt the addition of all the expansions of NP via the top-down rule, if we go that route. That is shown in the second chart snapshot after the first one.
If you want to stop the parse at any point, go to the file menu and just click “Reset Chart” – which, surprisingly, stops and resets the chart so that it is empty as at the beginning of a parse. The “Edit” menu lets you edit both the grammar and the sentence to parse, but you won’t need that for now. Let’s continue through with a top-down strategy (it will take several screenshots), and then look at a bottom-up strategy. After all that, we’ll finally get to some questions – so be patient…
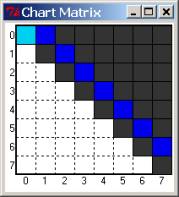
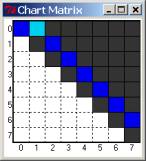
In addition to this chart window, the parser also displays in compact graphical form the chart graph as an n x n matrix, with the upper diagonal cells filled in with various informative colors. This is a useful aid to give an overall view as to how the parse is progressing, and where it might have gotten stuck. Initially, all cells are dark, with the one-off the main diagonal of the matrix is painted blue, corresponding to the words of the sentence to parse - since these are edges that span single positions. As a new edge is entered, it colors the cell it starts from light blue – this indicates what the parser is currently ‘working on’. As it finishes with a cell and moves on, the cell turns darker blue. If we reach the last [0,n] matrix entry with a valid S phrase, that cell turns green – indicating at least one good parse. See the pictures below.
Note
that if you do not care about animation, you can just unclick the ‘step’
button, check “No Animation” in the ‘Animate’ Menu, and then just hit the “Top
Down strategy” button. It will just run until done, and only then display
edges. It is much faster!
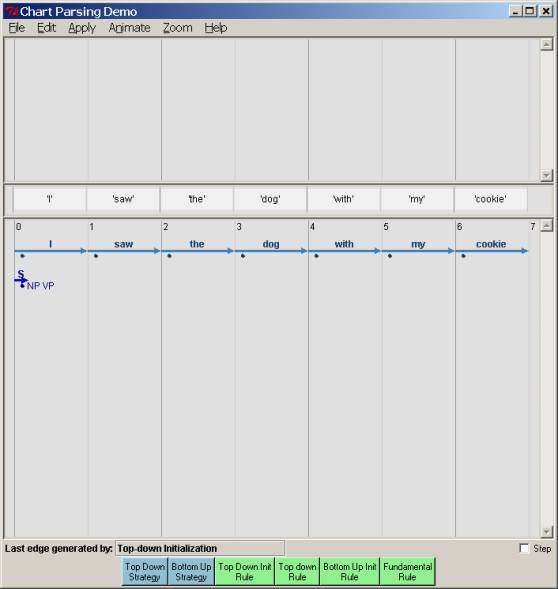
Chart cartoon corresponding to this picture:
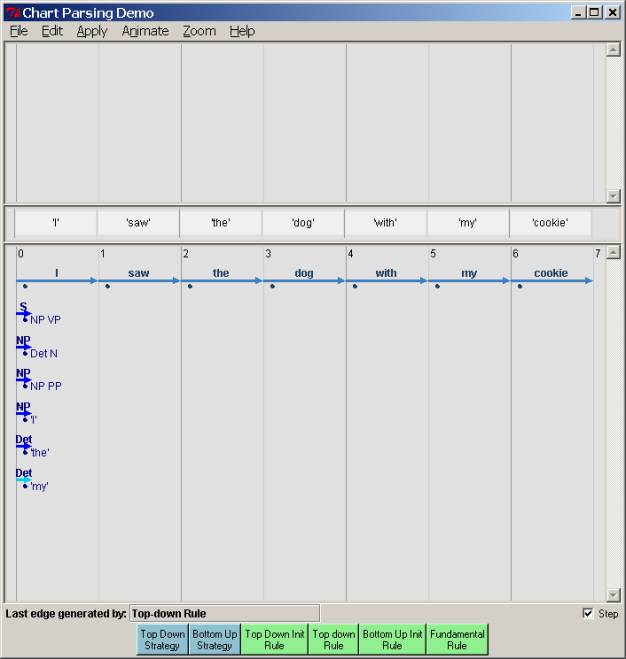
After all the top-down rule applications:
At this point, the fundamental rule can apply, because the word “I” can prompt the completion of the NP. Thus we can ‘jump’ the dot over the “I” and extend the edge for the NP from NP[0, 0] to NP[0, 1]:
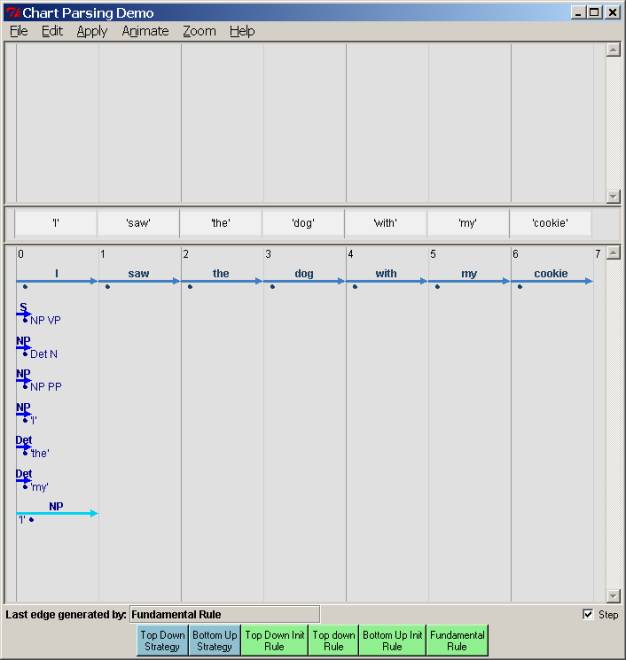
Chart cartoon matrix corresponding to this:
But since the NP is now complete, this also lets us ‘jump’ the dot over the S rule that was looking for an NP, and we can extend the “S” edge to S[0,1] – clearly not the end of the righthand side for S. In the log trace, we indicate this by the >, specifying that this is the righthand side so far.
The parse continues by running the top-down strategy (either by clicking the button or doing so automatically with animation) until we reach this end and no further top-down or fundamental rules can apply:
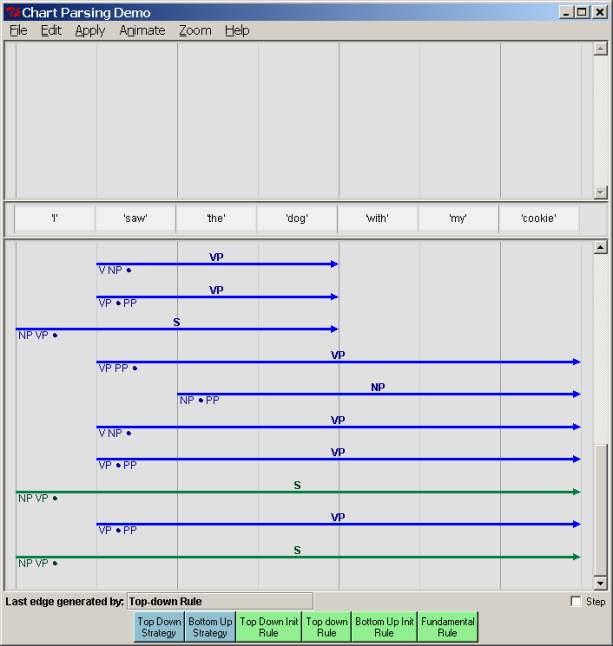
With
the corresponding chart matrix (note the green):
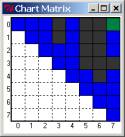
Clicking
on a complete S turns it red and displays the parse tree:
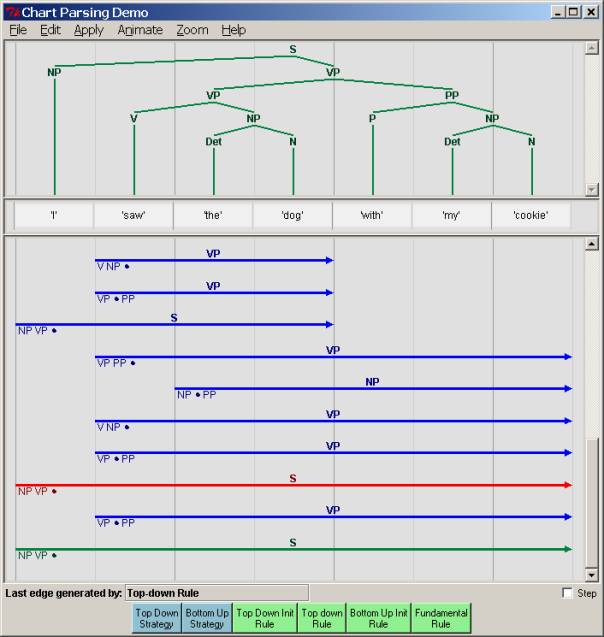
Clicking
on any other completed edge will display the subtree it spans, along with a
dotted line indicating any material that must come after the current dot
position (i.e., predicated material). Here we show the prediction of a PP after
a completed VP:
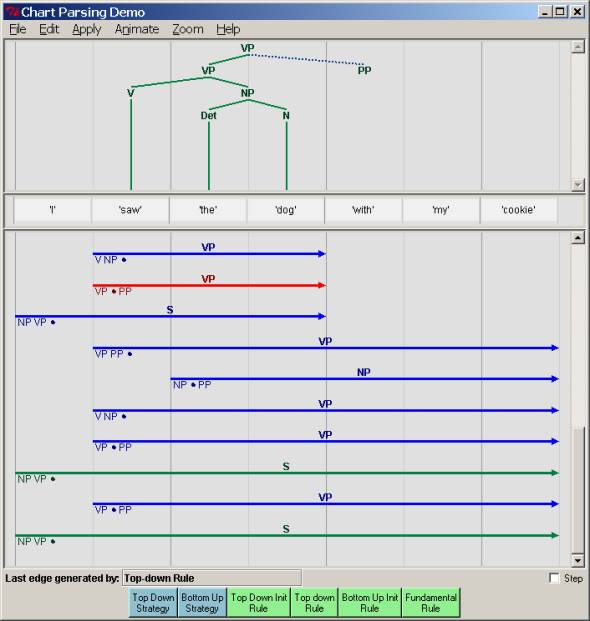
Now
let’s try the same sentence and grammar, but with a bottom-up strategy. We click on the “ Bottom up Init" Rule – this fills in the preterminal rule
edges:
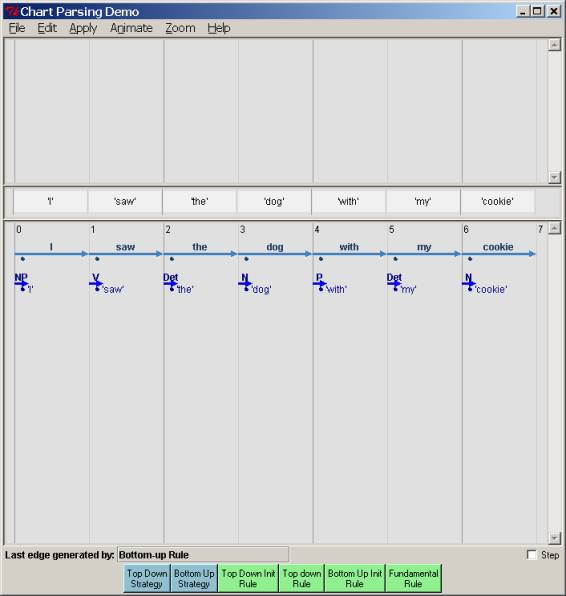
With
the corresponding chart matrix. You
should take note how the pattern of edge creation and matrix examination
differs between this approach and top-down parsing.
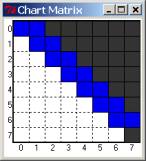
Here
we take a snapshot several steps into the parse – you can easily see that the
parse is proceeding from smaller pieces to larger (and not necessarily left to
right):
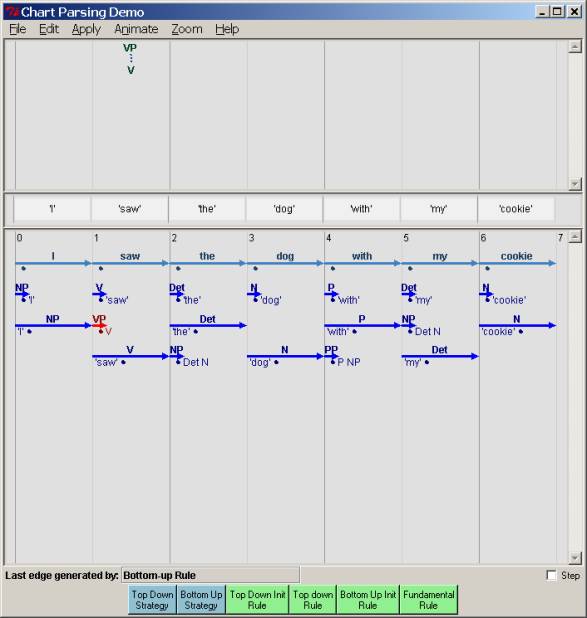
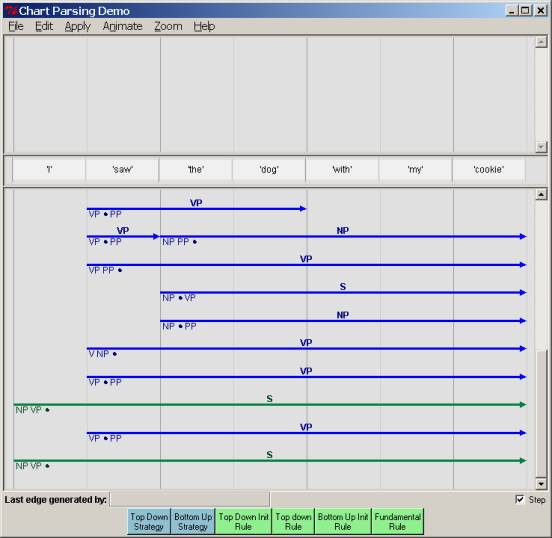
We get
the same final parses, as we should. But
you should also note that the pattern and kind of intermediate
edges created is different from the top-down parse. And that is our first question.
3. Questions on chart parsing
Please
login to Athena, add
6.863, and start up the chart parser.
It will be set with a demo grammar and sentence – “John ate the cookie
on the table” - not the one above. Carry out the top-down and bottom-up parsing
strategies as demonstrated above. You’ll have to run the parser several times
to answer the following questions. Remember that you don’t need to wait
for the animation – just make sure the step check box is not checked, and that
“No Animation” is selected in the ‘Animation’ Menu.
Question
5. The top-down and bottom-up strategies should get the same (two)
parses – check that this is so. BUT they do not do so by constructing
the same edges. Nor do they construct
the same number of edges. We can take the number of edges constructed as the
basic computational cost of this parsing method. (Remember the definition of an
edge: a line with a distinct label, a start, and a stop position.) Which
strategy constructs fewer edges, and roughly, by what percent (for this
sentence)? Please explain carefully
and precisely why one method is more efficient than the
other. Do you think this will hold
generally? Again explain why.
Question
6. Even though one method might be more
efficient than the other, it is still true that both construct edges that the
other one does not. Given our demo
example sentence “John ate…”, please give an example of an edge that the top-down
strategy constructs but the bottom-up strategy does not, and vice-versa. Then please explain for each of your
examples why its corresponding cousin parser does not generate
these edges – in other words, what information is each parser using that the other
does not, in order to weed out the edges that you just exhibited. (E.g., the
top-down parser produces edges the bottom-up one does not – so how is the
bottom-up strategy eliminating these edges?)
You
can precisely control which edge is selected for either top-down
or bottom-up rule processing by selecting it first with a mouse
click and then running either the top-down, bottom-up, or fundamental rule on
it by clicking just once on the appropriate button (you must have animation
turned off and the “step” box checked on.) This gives you very fine-grained control of
the parsing strategy, which you may need for the following problem.
Question
7. [Challenge problem for
everyone] Can you find a combination of top-down and bottom-up strategy
applications (you will also have to include judicious fundamental rule
applications) that is more efficient (= produces fewer edges) than
either the pure top-down or bottom-up method? If you can, then you ought to
be able to produce a final chart with fewer edges than either of these two,
just by punching the top-down and bottom-up buttons in the right order. See if you can find a parse that writes down
fewer edges – remember that you have to produce both possible parses.
(Hint: you might also want to think about the minimum number of distinct
edges required to describe both parse trees – plainly the number the parser
produces cannot be less than this.) As evidence, include a picture of the final
chart, the number of edges, and a brief description of your mixed strategy.(If
it’s not possible – illustrate the best ‘mixed’ strategy you can. You’ll have
to do X11 screenshots; we will probably also figure out a way to write out the
chart in something other than the format it has now, which is pcl. Don’t ask.)
4. Earley parsing: top-down parsing with bottom-up
filtering
As
Question 7 suggests, it would be nice to combine the best of both worlds from
top-down parsing and bottom-up parsing.
This goal is (mostly) attained by a context-free parsing method called Earley
parsing, after its author, Jay Earley.
Roughly, Earley parsing combines bottom-up parsing with top-down
filtering. This is described in detail in the notes referred to at the very
start of this Lab, so we won’t go into it further here. Instead, we’ll jump right into using our
chart-based implementation of Earley parsing.
There are a few GUI differences from the other parsers that you need to
attend to.
Running
the Earley parser
As
with the other parsers, once you have added 6.863, you can simply invoke the
Earley parser this way:
athena% cd /mit/6.863/python-earley
athena%
earley
This
will pull up the following window, in which you can load your own or a demo
grammar and lexicon, or just type one in.
Grammar files have the extension .grm. (These files are otherwise
just plain text files, so you can edit them any way you want – the Earley
window has a fairly complete editor so you can find/search & replace; and
so forth to edit a grammar file right there – but you should save the result in
your own dir.)
For
the lab, we want you to load a very, very simple test grammar in the python-earley
directory (you can play with others if you want). The file is lab3a.grm. To load it, simply go to the “File” menu, click “Open”, which will pull
up the list of .grm files in
the directory, and select lab3a.grm. Please do that now. Your window should now look like the one
below – if it doesn’t, something is awry and you should ask us! The format
shown below is what you should follow for this Lab part a: separate lines for
each rule; a separator between rules and lexicon. Note that a word can have
more than one part of speech. Also note
that the way we write the lexicon is a bit different from the chart parser –
just the word followed by one or more part of speech categories. (We have also
wired this parser so that it can accept Kimmo input, but that is a story for
another day.)
Important: Your grammar file should
always include at least one rule that is in the following form,
Start ® … ; for instance, Start ® S. The
order of rules in the Rules section does not matter. The order of lexical items in the Lexicon section does not
matter. Once you have loaded a rule file, you can parse a sentence by typing in
the sentence in the panel below the grammar, and then pressing “Parse”. This
will pull up a window similar to the chart windows for the previous examples,
but again different in a few details.
You can proceed to parse a sentence by hitting the “Run parser” button
on this new window. Again as before,
this will trace out the creation of each edge as it is placed into the chart.
The “Step” checkbox works as before – you can trace through parse execution,
edge by edge. There are no strategy
control buttons, because the whole point of the Earley algorithm is to fix a
particular strategy for edge construction.
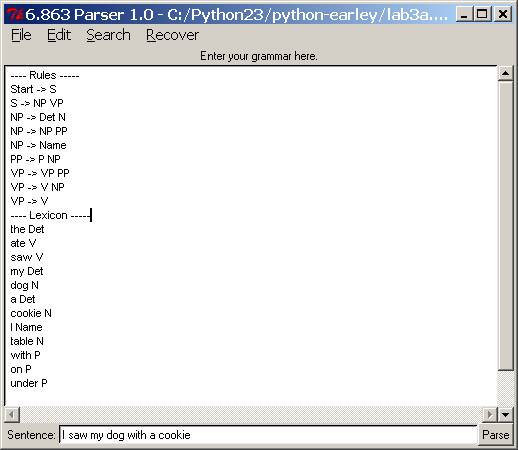
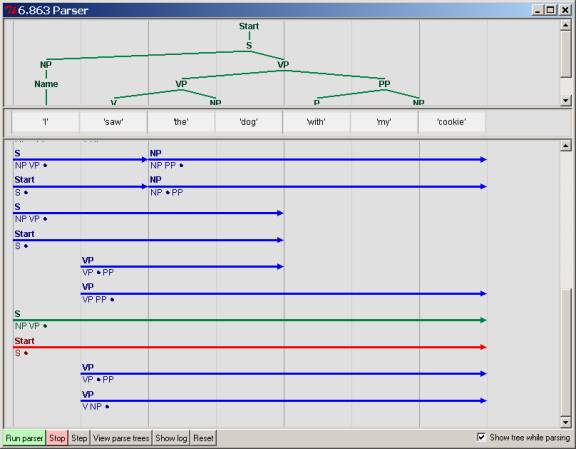
If the
parse is successful, a window will pop up with a tree display for the
parse. You can print this to
postscript. If there is more than one parse, you can scroll through them using
the “Next” and “Prev” buttons on the window,
inspecting or printing each one as you want
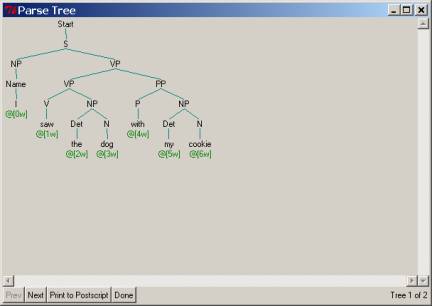
Pressing
the “Show Log” button will display the actual edges as they are created, their
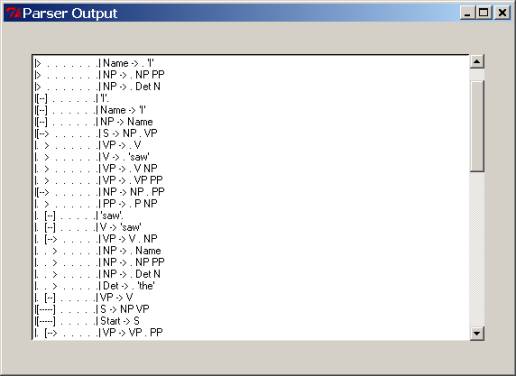
label, and their extent, as discussed in section 2.3. This is most helpful in
diagnosing exactly where a parse goes awry.
Question
8. Earley parsing efficiency. OK, since we’ve done all this work
with Earley parsing – does it accomplish our goal of reducing the number of
edges (what the Earley calls items) constructed for the parse of “I saw my dog
with a cookie”? Count the number of
edges and compare to both of the
earlier (heh) top-down and bottom-up chart parsing strategies. Which is best in this sense? If Earley does not achieve the most
efficient parse in terms of number of edges constructed, why not?
Question
9: Earley parsing and ambiguity. We
note that the chart is of quadratic size in the input sentence length,
since it is essentially (the upper triangular part) of an n x n matrix.
Additionally, since edge labels can only be drawn from the nonterminal and
terminal names of the grammar, whose size we call |G|, the matrix is more exactly
of size O( |G| n2 ). (Or even more precisely, about half that since we only fill the
upper part of the square chart matrix.)
As we noted in Question 7, however, the total number of distinct parse
trees that might be produced is superpolynomial. Thus, the chart matrix must somehow represent in a quadratic
space a superpolynomial number of
distinct trees. At first glance this
seems paradoxical. Please explain how this compaction is done by the chart data
structure, using as your example the final chart and the log of edge
construction for the sentence “I saw my dog with a cookie.”
Please be precise in your explanation by inspecting the log trace
carefully, and, if that trace does not fully account for how the alternative
parses are ‘compacted’ please describe what other data structures or
information would be needed to accomplish this. (You needn’t take more than a paragraph or two.)