In this section we prove a technical lemma that is needed for the proof of Lemma 3.4.
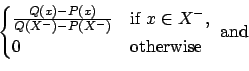 |
|||
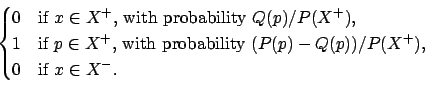 |
It is easy to check that ![]() is indeed a distribution over
is indeed a distribution over ![]() (with support set
(with support set ![]() ).
).
Let ![]() and
and ![]() be independent random variables from distributions
be independent random variables from distributions
![]() and
and ![]() , respectively. Now define
, respectively. Now define ![]() as follows:
as follows:
We claim that the such defined ![]() is suitable. Indeed, by Equation
13
is suitable. Indeed, by Equation
13
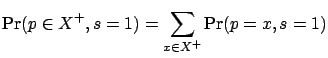 |
|||
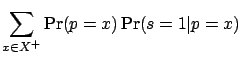 |
|||
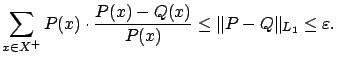 |
Furthermore,
We calculate each term of Equation 14 separately, both for
![]() and
and ![]() . First assume that
. First assume that ![]() . Then
. Then
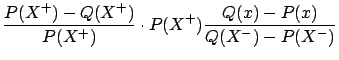 |
|||
Now let us consider the case ![]() .
.
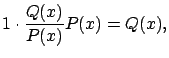 and and |
|||
In both cases we get
![]() , which was to be proven.
, which was to be proven.
![]()