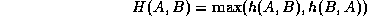



Design and implementation of the system described requires solution to a number of challenging problems. First, the system must be robust, tolerate a small area of fundus illumination, and respond rapidly to moderate changes in eye position during evaluation and treatment. We approach this by acquiring multiple, partially overlapping photographic images and montaging these images in non-real-time. Available angiographic and photographic data will be registered with the montaged data set to allow for rapid rendering. Since photographic and angiographic data may vary considerably in intensity, e.g. the blood vessels are dark in a monochromatic image and in the early angiographic phases but bright in the late angiographic phase, intensity based registration algorithms are unsuitable. We are exploring edge-based registration algorithms, and have demonstrated successful image registration of color, monochromatic, and angiographic data following image pre-processing with smoothing, edge detection, and thresholding. The real-time fundus image will then be registered in near-real time with the montaged data set.
Next, the stored data must be ``overlayed'' on the biomicroscopic image. The computer rendering must be fast, and ergonomically well-tolerated. Lastly, technologies permitting interactivity will be developed. A remote observer (e.g. an expert supervising the local examiner, or a trainee ``observing'' a diagnostic or therapeutic maneuver) will view a real-time graphical display of the biomicroscopic image, and will be able to communicate questions or recommendations by text or voice. The remote observer will control a mouse-based ``virtual pointer'' to unambiguously identify regions of interest. The local user will similarly control a pointer to enable distance and area measurements, the results of which will be displayed in the text window. With both the local and remote user in control of a pointer, and able to communicate by voice or text, interactivity is facilitated.
An appropriate similarity metric for registration and montaging functions must be chosen. The ``Hausdorff distance'' (Huttenlocher et al., 1993; Rucklidge, 1995) is well-suited for our purposes since it a) runs well for edge-detected images, b) tolerates errors as well as the presence of extra or missing data points between data sets, and c) operates on an arbitrary, user-defined transformation function. For matching the fundus images, we are searching only over translation, rotation, and scale.
The Hausdorff distance is computed only for positively thresholded (e.g. edge-detected) points and is defined by
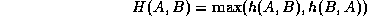
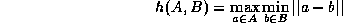
where ||a-b|| represents Euclidean distance.
The Hausdorff distance identifies the point 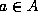 that is farthest
from any point of B, and measures the distance from a to its nearest
neighbor in B. Equivalently, if
that is farthest
from any point of B, and measures the distance from a to its nearest
neighbor in B. Equivalently, if 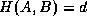 , then
, then
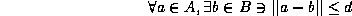
or all points in A must be within a distance d from some point in B, with the most mismatched point at exactly a distance d from the nearest point in B.
Due to occlusion and outliers, not all points in A will have a meaningful correspondence with a point in B. We therefore use the partial Hausdorff distance measure:
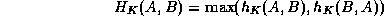
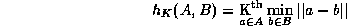
An extension of the Hausdorff distance by Huttenlocher et al. (1993) defines
a fraction of points in set A that lie within  of some
point in B:
of some
point in B:
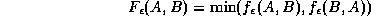
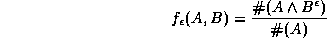
where 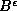 is the point set B dilated by
is the point set B dilated by  , or
the Minkowski sum of B with a disk of radius
, or
the Minkowski sum of B with a disk of radius  . In
other words,
. In
other words, 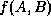 is the fraction of points in A that lie within
is the fraction of points in A that lie within
 of some point in B. Instead of fixing K and minimizing
of some point in B. Instead of fixing K and minimizing
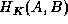 , we fix the dilation
, we fix the dilation  and maximize
and maximize 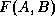 .
.
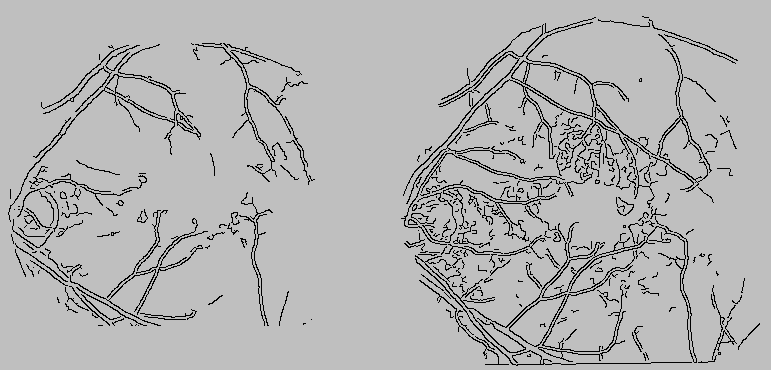
Figure: Binarized images of the
monochromatic (left) and angiographic (right) images depicted in
Figure 1. Edges were found using the Canny
edge detector.


