Problem
Image-guided neurosurgery relies on accurate registration between preoperative image volumes and images that are acquired throughout the surgery, as the brain deforms after the opening of the dura and the resection of the tumor. Preoperative imaging techniques provide critical information for the neurosurgeon that cannot be practically obtained during the surgery. Registration requires estimating, tracking, and characterizing complex shapes and motions in order to best deform the preoperative image volumes to match the intraoperative images. In such applications, physics-based deformable modeling provides an appropriate mechanism for modeling tissue properties and estimating the motion. Accurate registration results therefore depend on the quality of the model. As the brain is better represented, the results, and our confidence in them, should be improved.
Approach
The approach was to use a Finite Element (FE) discretization, by constructing an unstructured grid representing the geometry of key brain structures in the intraoperative dataset, in order to model important regions while reducing the number of equations that need to be solved. The rapid execution times required by neurosurgical operations were achieved by using parallel hardware configurations, along with parallel and efficient algorithm implementations.
The linear elastic Finite Element model implementation was extended to allow for inhomogeneity and anisotropy according to the diffusion tensor data. DT-MRI provides magnitude and directional information of the diffusion of water, which has been shown to correspond to the anisotropy of brain tissue. Local elasticity parameters are calculated from the degree of anisotropy of the corresponding voxels, the direction of the anisotropy, and input material parameter estimates.
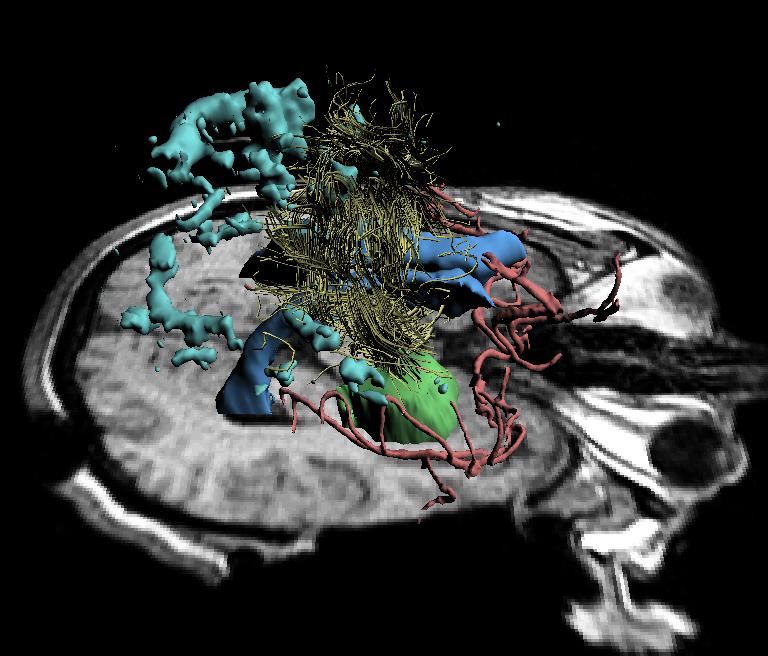
The deformation of the brain is rapidly and accurately captured during neurosurgery using intraoperative images and the biomechanical registration algorithm. This model has allowed us to align preoperative data to volumetric scans of the brain acquired intraoperatively, and thus to improve intraoperative navigation by displaying brain changes in three dimensions to the surgeon during the procedure. An example of this intraoperative visualization is shown in the figure below.

Future Work
There should be additional verification and evaluation of the model with more surgical cases, particularly those with larger amounts of brain shift. Identification of a greater number of landmarks would provide greater confidence in the registration accuracy differences. Additionally, a DT-MRI scan acquired at the end of the procedure would make it possible to compare the actual deformation of the white matter tracts to the model's prediction.
Next, the relationship that we define between the anisotropic tissue stiffness and the diffusion tensor is a simple linear mapping based on the fractional anisotropy. This is likely not how the diffusion tensor and the elasticity parameters are related, and more comprehensive studies could be used to improve this calculation. Intraoperative measurement of brain material properties would also allow for a more accurate modeling.
The model itself could also be further extended to use more complex material equations. As more powerful computers become available, these models become computationally feasible even given the time constraints of the neurosurgical procedure.
Simon K. Warfield warfield@bwh.harvard.edu
Ion-Florin Talos talos@bwh.harvard.edu
Back to the MIT AI Lab page.