In a 1975 paper [], Donald E. Knuth asserted (without further citation) that at that time computer manufacturers believed that about a quarter of computer time was spent sorting. Regardless of whether that fraction was true then, or what that fraction would be today, sorting is an example of software algorithms as technology. A civil engineer chooses from a wide variety of different building material technologies (e.g., wood frame, reinforced concrete, steel I-beam), based on the desired tradeoffs between cost, aesthetics, and strength, which depend on the needs of the particular project. A software engineer similarly chooses from a wide variety of different sorting algorithms based on the desired tradeoffs between coding complexity, suitability to size of problem (i.e., internal vs. external sorts), average space consumption, average time consumption, variability of space/time consumption, and sort stability. In both fields, particular technologies are refined over time, and new technologies may be created with potentially completely different tradeoffs. Taking advantage of evolutionary and revolutionary changes in sorting technologies sounds like fertile ground for a clever compiler.
The eqntott application from the SPECint92 suite of benchmarks [] translates a logical representation of a boolean equation to a truth table. It includes the following characterization in its description:
This characterization of eqntott execution is strictly speaking correct but rather misleading. Using gprof profiling, we see that although eqntott does spends about 90% of its time executing qsort(), about 85% of the total run-time was actually spent in cmppt(), which is only called from one particular call site of qsort().
The source code files for eqntott include an implementation for
qsort(), which makes sense, since the stability of standard C
library qsort() --- that is, whether it will or will not
preserve the initial ordering of elements being sorted which compare
as equal --- is intentionally undefined. By including its own
qsort(), those who submitted eqntott to the SPEC organization
as a benchmark could provide a reference output file to go with the
reference input file; whereas if eqntott used the
system
qsort(),
then the reference output file might not match eqntott's output
on a given platform even though the difference would be entirely due
to sort stability, and would not make the resulting output
incorrect. Since the qsort() routine supplied with eqntott
dates back to at least 1983 (it claims to be better than the system
qsort() of the day...), I was curious if qsort()
implementations had noticeably improved since then. Forcing
eqntott to use the system qsort() under SunOS 4.1.3 resulted in
nearly identical timings as using the included qsort(); however,
forcing eqntott to use the system qsort() on Linux
dramatically reduced run-time, from just over 20 seconds to 2.4
seconds.
Investigation readily uncovered that the Linux system qsort() is
supplied by the GNU implementation of the libc library; by
default, it does not use the quicksort algorithm, but rather uses the
merge sort algorithm if it can allocate enough temporary buffer to
perform a standard two-space merge sort, only falling back to an
in-place quicksort if the attempt to allocate memory fails. Both
merge sort and quicksort are on average O(N log N) algorithms;
however, in the real world, constant factors and not just asymptotic
algorithmic complexity matters. It is generally acknowledged that
implementations of some of the quicksort variants have the lowest
constant factors of well-known comparison-based sorting routines; this
is borne out by some basic experimentation --- each row of
Table 
was generated by summing the times and
comparisons for 5 different runs, each run sorting 1,000,000 integers
generated by random() with seed values 0, 1, 2, 3, and 4
respectively. (Times were quite consistent for runs which used the
same sort and had the same sortedness of input, differing only on the
random seed.)
Table: Merge sort and median-of-3 quicksort on arrays of integers.
So if the particular quicksort implementation beats the merge sort
implementation on both randomized and on already-sorted inputs, what
accounts for the nearly an order of magnitude difference in
eqntott performance? (A difference in the wrong direction to boot:
Table would suggest that eqntott using
quicksort would be faster than eqntott using merge sort,
when in fact the reverse is true.) One possibility is that most
analyses of sort algorithms assume that comparisons take constant
time; this is not always true. In particular, every comparison
routine defined in eqntott may take variable amounts of time to
execute. Hence it can matter greatly to the total run-time exactly
which elements are compared with each other, something which was not
true for sorting integers. I.e., one hypothesis is that in this case
merge sort tends to be comparing elements which the comparison routine
can quickly decide whether a<b, a=b, or a>b, whereas quicksort
tends to be comparing elements which the comparison routine cannot
quickly determine the ordering relationship. It should be noted that
such comparison functions are not particularly unusual: an ordering
string comparison function, for example, takes variable time to run,
being highly dependent on the nature of input data.
As attractive a hypothesis as this might be, however, it does not
stand up to scrutiny. In particular, profiling indicates that there
is a 79-fold reduction in the number of calls to cmppt():
quicksort calls it 2,841,621 times; merge sort, a mere 35,944 times.
That is responsible for the reduced run time for eqntott,
and not a hypothesized reduction in the average latency for a call to
cmppt(). The eqntott call site to qsort() which
provides cmppt() as a comparison function hands qsort() an
array with just 4,106 items; note that 2,841,621 comparisons to sort
4,106 items seems more nearly O(N
), despite the fact that the
quicksort implementation does have the median-of-3 modification which
should prevent most (but clearly not all) cases of such degenerate
behavior. The number of calls to cmppt() which the merge sort
issues, on the other hand, seems much closer to O(N log N). Is the
SPECint92 reference input file particularly unusual in eliciting this
kind of behavior from the quicksort implementation?
This kind of effort with blind alleys, hypotheses to shoot down, etc.,
is typical of of a human programmer attempting to optimize a program.
If the system qsort() had been written with a qif
statement to quasistatically select between a quicksort implementation
or a merge sort implementation, it would not be necessary to go to
this kind of effort, nor necessary to speculate about whether
typical user files provided as input to eqntott tend to elicit
O(N
) behavior from the quicksort used; whether or not quicksort
often behaved poorly or not on user inputs would be directly observed
and taken into account. Furthermore, casual trials with another
similarly-sized input file for eqntott (modeling a 4-bit
16-input/output multiplexer) suggests that the reference input file
for the SPECint92 benchmark use of eqntott is in fact somewhat
anomalous for eliciting such poor behavior from quicksort; however,
program performance for the multiplexor input file was still about
20% better with merge sort than with quicksort, consistent with the
results in Table which shows that the merge
sort implementation tends to perform fewer comparisons --- and
the number of comparisons, when each comparison can be quite
expensive, will dominate the running time more than the efficiency of
the inner loops of the sorting algorithm. Hence which sort should be
selected in a given usage will depend on both the input data pattern
and on the cost of the comparison function provided to qsort().
To reiterate, if the library writer had written the system
qsort() with a qif statement, then sorting performance would be
improved on average, without any effort from the application
programmer's part and without complicating the semantics of
qsort() usage.
Another obvious approach to improving the performance of eqntott
would be to try to make cmppt() execute faster.
Figure shows the inner loop of the
comparison function. It's not hard to convince oneself that the code
in Figure is equivalent
Figure , but might execute faster on
average if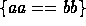 
, 
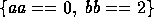, or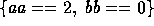 
were common conditions. However, it's unclear which of the three
terms should come first in the conditionally evaluated boolean-OR
expression for best performance; presumably, this is dependent on the
input to eqntott. It would be highly tedious to try them all
out by hand; but a quasistatic compiler would not be deterred by
impatience. With quasistatic if support, the programmer can
simply write the code sequence in Figure and
forget about it. Note the total number of permutations is
actually far greater than the three which happen to be shown: the
three clauses OR'ed together can be arranged 6 different ways; plus,
each of the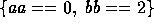 
and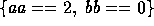 
clauses contains
two sub-clauses AND'ed together, which can also be permuted --- for a
total of 24 possible versions.
Figure: Comparison routine cmppt()'s inner loop.
Figure: A restructuring of the cmppt() inner loop.
Figure: Quasistatic version of cmppt() inner loop.
Table: Performance of different rearrangements of boolean terms.
Table shows the performance numbers for a
few of the possible versions; only one of the listed versions performs
better than the original version. Note that careless use of
quasistatic constructs in tight inner loops resulted in
spectacular profiling overhead, far greater than even that for
pixie. This is in part because the current real-time profiling
implementation does not customize the stopwatch start and stop
routines for each place where they are used, even though they are
inlined; hence the routines still have greater overhead than
pixie's instrumentation code per invocation. Furthermore, it so
happens that the problem is vastly excaberated by the fact that the
current implementation of real-time profiling has a bug whereby the
GNU gcc code generator believes two registers contain live data
between the stopwatch start and stop routines, and this causes several
of the inner loop variables to be spilled from the unusually small
register set of the Intel Pentium processor. Fortunately, the
overhead did not in this case mask which alternative would run faster
when instrumentation is turned back off. We see that although there
is some improvement, the cmppt() comparison function did not
offer great opportunity for optimization using quasistatic constructs.
However, it does serve as an example where the programmer can use the
clever compiler's capabilities as a tool to simplify the task of
exploring what-if scenarios to improve program performance, although
judiciously (i.e., not in inner loops). It's less tedious and less
error-prone to let the clever compiler manage program versions than to
do so by hand.
Several other possible transformations to improve eqntott
performance, which might benefit from quasistatic constructs, were not
fully explored for lack of time. They are described in
Appendix .
