



Next: Conclusions
Up: Examples
Previous: eqntott (SPECint92)
Much of scientific and engineering computation boils down to
calculations based on linear systems of equations, commonly
represented as matrices. Hence there is great interest in developing
sophisticated packages with routines carefully tuned for
accuracy and performance. Numerical Recipes
[], a popular resource for those interested in
numerical computation, mentions that such packages (e.g., LINPACK,
NAG) often provide many versions of particular routines, which are
specialized for special matrix forms (e.g., symmetric, triangular,
etc.) and perform faster than the generalized routine on such cases.
One can imagine coding using predicates to check for special forms and
thus taking advantage of special form routines, even when one is
uncertain in advance what special forms the matrices being dealt with
might conform to --- see Figure
and performance. Numerical Recipes
[], a popular resource for those interested in
numerical computation, mentions that such packages (e.g., LINPACK,
NAG) often provide many versions of particular routines, which are
specialized for special matrix forms (e.g., symmetric, triangular,
etc.) and perform faster than the generalized routine on such cases.
One can imagine coding using predicates to check for special forms and
thus taking advantage of special form routines, even when one is
uncertain in advance what special forms the matrices being dealt with
might conform to --- see Figure  .
.
Is coding in this fashion worthwhile? Suppose in writing numeric
crunching applications, the programmer absolutely knows if matrix
A is going to take on a special form or not. If so, then testing at
all is completely pointless --- the programmer can directly call the
the correct special form routine, or the general routine if no special
forms apply. However, if there is some uncertainty in the
programmer's mind, as is likely to be the case for example with
someone writing an application-area-specific library, then which
strategy --- Figure  ,
Figure
,
Figure  , or just always calling
LU_decompose_general() directly --- gives the best performance
requires more careful consideration. The writers of libraries such as
LINKPACK and NAG were presumably reluctant to put in additional
``unnecessary'' checking overhead into the general routines
themselves, thinking ``Why should we slow down the general library
routine with checks for special cases every time, especially if the
general form algorithm will always give the correct answer anyway?
Let the user check for special cases and call the specialized routines
if they want.'' However, the user may similarly be reluctant to slow
down his or her code by writing something like
Figure
, or just always calling
LU_decompose_general() directly --- gives the best performance
requires more careful consideration. The writers of libraries such as
LINKPACK and NAG were presumably reluctant to put in additional
``unnecessary'' checking overhead into the general routines
themselves, thinking ``Why should we slow down the general library
routine with checks for special cases every time, especially if the
general form algorithm will always give the correct answer anyway?
Let the user check for special cases and call the specialized routines
if they want.'' However, the user may similarly be reluctant to slow
down his or her code by writing something like
Figure  . Even if each of the
is_*_matrix() predicate functions takes just O(
. Even if each of the
is_*_matrix() predicate functions takes just O(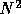 ) execution time,
string enough tests together and there will be noticeable slow-down.
) execution time,
string enough tests together and there will be noticeable slow-down.
On the other hand, in the quasistatic version in
Figure  , only if matrix A is
often one of the special forms will the price of even a single test
continue to be paid at equilibrium (e.g., after the initial
experimentation phase); and, if matrix A is not any of the
special forms being tested for, then no testing for special
forms will be performed at all at equilibrium. Furthermore, note that
the typical input matrix might be simultaneously several special
forms, and in such cases the quasistatic version would automatically
pick out the specialized routine that performs the best on the
statistically likely inputs. However, the quasistatic version has the
draw-back that if the input matrix is one special form about half the
time and another special form the other half of the time (i.e., the
entropy of the question ``What special form is this matrix?'' is
high), then for Figure
, only if matrix A is
often one of the special forms will the price of even a single test
continue to be paid at equilibrium (e.g., after the initial
experimentation phase); and, if matrix A is not any of the
special forms being tested for, then no testing for special
forms will be performed at all at equilibrium. Furthermore, note that
the typical input matrix might be simultaneously several special
forms, and in such cases the quasistatic version would automatically
pick out the specialized routine that performs the best on the
statistically likely inputs. However, the quasistatic version has the
draw-back that if the input matrix is one special form about half the
time and another special form the other half of the time (i.e., the
entropy of the question ``What special form is this matrix?'' is
high), then for Figure  the clever
compiler must choose the clause for one of the special forms over the
other; however, better performance could be had by pay the price of an
extra testing predicate to test for both equally-likely special forms
before defaulting to the general form. It would be advantageous to at
least include one more clause, which simply contains the chain of
tests in Figure
the clever
compiler must choose the clause for one of the special forms over the
other; however, better performance could be had by pay the price of an
extra testing predicate to test for both equally-likely special forms
before defaulting to the general form. It would be advantageous to at
least include one more clause, which simply contains the chain of
tests in Figure  .
. Also, whereas in Figure
Also, whereas in Figure  ,
the price for considering another special form is O(
,
the price for considering another special form is O(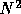 ) during
every execution of this piece of code, the price in the quasistatic
case is that there are more versions of the program for the clever
compiler to try out, and it will therefore take longer for the clever
compiler to converge on a reasonably optimal program.
) during
every execution of this piece of code, the price in the quasistatic
case is that there are more versions of the program for the clever
compiler to try out, and it will therefore take longer for the clever
compiler to converge on a reasonably optimal program.

Figure: Selecting at run-time between all the special-case matrix routines.

Figure: Quasistatically selecting between special-case matrix routines.
A well-known optimization technique is blocking: given multiple levels
of memory hierarchies with different latencies, blocking improves the
reuse of data loaded into the faster levels of the hierarchy and thus
overall program throughput. One application of blocking is to matrix
multiplication: Figure  contains a
simple implementation of blocked matrix multiplication for
illustration purposes. In essence, the BlockedMultiply routine
takes an
contains a
simple implementation of blocked matrix multiplication for
illustration purposes. In essence, the BlockedMultiply routine
takes an 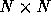 matrix and chops it up into blocks of size
matrix and chops it up into blocks of size 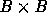 ; at any given time, the routine places less demand on the
cache than an unblocked version because in the innermost loop, it is
only accessing information from
; at any given time, the routine places less demand on the
cache than an unblocked version because in the innermost loop, it is
only accessing information from 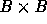 -sized sub-matrices
(blocks) of the source matrices X and Y and the destination matrix
Z. [] observes that in the worst case (no blocking),
-sized sub-matrices
(blocks) of the source matrices X and Y and the destination matrix
Z. [] observes that in the worst case (no blocking),
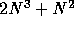 words may have to be accessed from main memory, but if B
is chosen such that the
words may have to be accessed from main memory, but if B
is chosen such that the 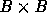 block of Y and a row of length
B of matrix Z can fit in the cache without interference, then the
number of memory accesses drops to
block of Y and a row of length
B of matrix Z can fit in the cache without interference, then the
number of memory accesses drops to 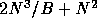 . Clearly, then, it is
desirable to maximize the value of B; the speed of microprocessors
has increased to the point in the last few years where the number of
main memory accesses (i.e., cache misses) and not the actual
computation on the data retrieved can prove to be the performance
bottleneck. [] goes on to develop models of cache
interference for such blocked algorithms, to come up with a more
sophisticated way of choosing the block size to maximize reuse; the
rationale for such work is that simply choosing B such that a
. Clearly, then, it is
desirable to maximize the value of B; the speed of microprocessors
has increased to the point in the last few years where the number of
main memory accesses (i.e., cache misses) and not the actual
computation on the data retrieved can prove to be the performance
bottleneck. [] goes on to develop models of cache
interference for such blocked algorithms, to come up with a more
sophisticated way of choosing the block size to maximize reuse; the
rationale for such work is that simply choosing B such that a 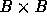 block plus a row of length B might just barely fit within
the cache (i.e., considering size only) was demonstrated to be
inadequate, as data self-interference under certain cirumstances
greatly reduced the cache hit rate and thereby the effective
throughput [].
block plus a row of length B might just barely fit within
the cache (i.e., considering size only) was demonstrated to be
inadequate, as data self-interference under certain cirumstances
greatly reduced the cache hit rate and thereby the effective
throughput [].

Figure: Blocked matrix multiply implementation.
The results in Table  show (for both integer and
double-precision floating point numbers) that as the blocking size
increases, the number of CPU cycles elapsed before the computation
finishes decreases nearly monotonically, with most of the performance
benefit achieved at relatively small values for the block size.
Surprisingly, even after I went past the block size that should have
meant the the cache had to have overflown (for example, the integer
B=256 case should have just about overflowed the cache, since
show (for both integer and
double-precision floating point numbers) that as the blocking size
increases, the number of CPU cycles elapsed before the computation
finishes decreases nearly monotonically, with most of the performance
benefit achieved at relatively small values for the block size.
Surprisingly, even after I went past the block size that should have
meant the the cache had to have overflown (for example, the integer
B=256 case should have just about overflowed the cache, since
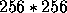 32-bit integers take up 256KB of memory), we see that the
performance was hardly impacted at all when we moved to B=512. This
argues for experimental verification of timings on actual machines
where the code will be run, as this is an result that would not have
been expected from the models --- my speculation is that the cache
pre-fetch was sufficiently effective on this machine that the
additional memory demands of too-large a blocking size did not create
a bottleneck. In any case, the clever compiler, when allowed to
choose from a wide range of blocking values as expressed by a
qint parameter, can experimentally determine that it is safe to use
very large blocks. However, another machine which was also
i386-binary compatible, but with different latencies and bandwidths
for transfers between the cache and main memory, might well have
choked on the larger block values, hence it is desireable to set the
block size quasistatically and not statically.
32-bit integers take up 256KB of memory), we see that the
performance was hardly impacted at all when we moved to B=512. This
argues for experimental verification of timings on actual machines
where the code will be run, as this is an result that would not have
been expected from the models --- my speculation is that the cache
pre-fetch was sufficiently effective on this machine that the
additional memory demands of too-large a blocking size did not create
a bottleneck. In any case, the clever compiler, when allowed to
choose from a wide range of blocking values as expressed by a
qint parameter, can experimentally determine that it is safe to use
very large blocks. However, another machine which was also
i386-binary compatible, but with different latencies and bandwidths
for transfers between the cache and main memory, might well have
choked on the larger block values, hence it is desireable to set the
block size quasistatically and not statically.
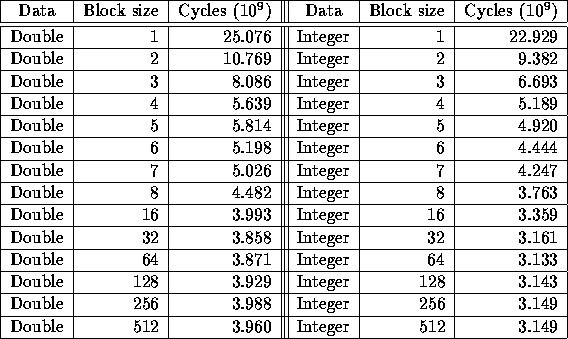
Table: Multiplying 512x512 matrices with different block sizes.
Table  generally corroborates the conclusion
that large block sizes are quite safe on this machine; the details
demonstrate that measuring elapsed real time rather than UNIX process
user time can be important, because they sometimes tell different
stories. Certain values for block size (e.g., B=5, B=6, B=7)
resulted in drastically poorer elapsed real time performance as
compared to neighboring block sizes (mostly due to delays due to page
faults), although their user times continued to drop monotonically;
somewhat surprising, though, is the elapsed real time performance drop
at B=320. (Ironically, B=320 achieved one of the best user times
in the table.) A sophisticated model which was given the exact
parameters for the virtual memory subsystem for the operating system
kernel might or might not have anticipated this lattermost result;
however, experimentation by the clever compiler would have revealed it
without the need for such detailed knowledge. Another example of the
utility of performing measurements of real time as well as user time
is comparing B=256 and B=1280: although B=256 took nearly 50
seconds less user time, B=1280 caused sufficiently fewer page faults
that it was faster in terms of elapsed time by about 3.25 billion
cycles, or about 36 seconds. On this machine B=128 appears to be
the overall the fastest, combining the three criteria real time, user
time, and page faults; however, on a similar machine outfitted with
more or less memory, or on a machine which was configured to swap over
the network, a different value might have proved to be optimal.
generally corroborates the conclusion
that large block sizes are quite safe on this machine; the details
demonstrate that measuring elapsed real time rather than UNIX process
user time can be important, because they sometimes tell different
stories. Certain values for block size (e.g., B=5, B=6, B=7)
resulted in drastically poorer elapsed real time performance as
compared to neighboring block sizes (mostly due to delays due to page
faults), although their user times continued to drop monotonically;
somewhat surprising, though, is the elapsed real time performance drop
at B=320. (Ironically, B=320 achieved one of the best user times
in the table.) A sophisticated model which was given the exact
parameters for the virtual memory subsystem for the operating system
kernel might or might not have anticipated this lattermost result;
however, experimentation by the clever compiler would have revealed it
without the need for such detailed knowledge. Another example of the
utility of performing measurements of real time as well as user time
is comparing B=256 and B=1280: although B=256 took nearly 50
seconds less user time, B=1280 caused sufficiently fewer page faults
that it was faster in terms of elapsed time by about 3.25 billion
cycles, or about 36 seconds. On this machine B=128 appears to be
the overall the fastest, combining the three criteria real time, user
time, and page faults; however, on a similar machine outfitted with
more or less memory, or on a machine which was configured to swap over
the network, a different value might have proved to be optimal.
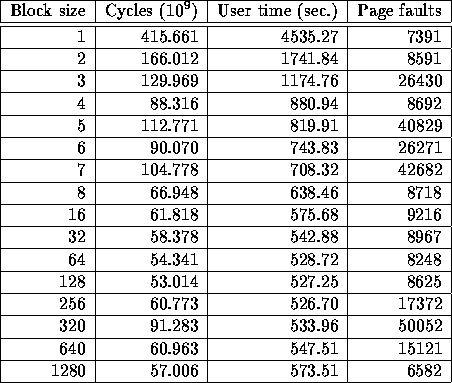
Table: Multiplying 1280x1280 integer matrices with different block sizes.




Next: Conclusions
Up: Examples
Previous: eqntott (SPECint92)
Reinventing Computing, MIT AI Lab. Author: pshuang@ai.mit.edu (Ping Huang)
 and performance. Numerical Recipes
[], a popular resource for those interested in
numerical computation, mentions that such packages (e.g., LINPACK,
NAG) often provide many versions of particular routines, which are
specialized for special matrix forms (e.g., symmetric, triangular,
etc.) and perform faster than the generalized routine on such cases.
One can imagine coding using predicates to check for special forms and
thus taking advantage of special form routines, even when one is
uncertain in advance what special forms the matrices being dealt with
might conform to --- see Figure
and performance. Numerical Recipes
[], a popular resource for those interested in
numerical computation, mentions that such packages (e.g., LINPACK,
NAG) often provide many versions of particular routines, which are
specialized for special matrix forms (e.g., symmetric, triangular,
etc.) and perform faster than the generalized routine on such cases.
One can imagine coding using predicates to check for special forms and
thus taking advantage of special form routines, even when one is
uncertain in advance what special forms the matrices being dealt with
might conform to --- see Figure  .
.




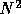 ) execution time,
string enough tests together and there will be noticeable slow-down.
) execution time,
string enough tests together and there will be noticeable slow-down.
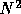 ) during
every execution of this piece of code, the price in the quasistatic
case is that there are more versions of the program for the clever
compiler to try out, and it will therefore take longer for the clever
compiler to converge on a reasonably optimal program.
) during
every execution of this piece of code, the price in the quasistatic
case is that there are more versions of the program for the clever
compiler to try out, and it will therefore take longer for the clever
compiler to converge on a reasonably optimal program.


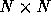 matrix and chops it up into blocks of size
matrix and chops it up into blocks of size 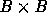 ; at any given time, the routine places less demand on the
cache than an unblocked version because in the innermost loop, it is
only accessing information from
; at any given time, the routine places less demand on the
cache than an unblocked version because in the innermost loop, it is
only accessing information from 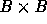 -sized sub-matrices
(blocks) of the source matrices X and Y and the destination matrix
Z. [
-sized sub-matrices
(blocks) of the source matrices X and Y and the destination matrix
Z. [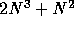 words may have to be accessed from main memory, but if B
is chosen such that the
words may have to be accessed from main memory, but if B
is chosen such that the 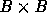 block of Y and a row of length
B of matrix Z can fit in the cache without interference, then the
number of memory accesses drops to
block of Y and a row of length
B of matrix Z can fit in the cache without interference, then the
number of memory accesses drops to 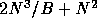 . Clearly, then, it is
desirable to maximize the value of B; the speed of microprocessors
has increased to the point in the last few years where the number of
main memory accesses (i.e., cache misses) and not the actual
computation on the data retrieved can prove to be the performance
bottleneck. [
. Clearly, then, it is
desirable to maximize the value of B; the speed of microprocessors
has increased to the point in the last few years where the number of
main memory accesses (i.e., cache misses) and not the actual
computation on the data retrieved can prove to be the performance
bottleneck. [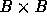 block plus a row of length B might just barely fit within
the cache (i.e., considering size only) was demonstrated to be
inadequate, as data self-interference under certain cirumstances
greatly reduced the cache hit rate and thereby the effective
throughput [
block plus a row of length B might just barely fit within
the cache (i.e., considering size only) was demonstrated to be
inadequate, as data self-interference under certain cirumstances
greatly reduced the cache hit rate and thereby the effective
throughput [
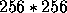 32-bit integers take up 256KB of memory), we see that the
performance was hardly impacted at all when we moved to B=512. This
argues for experimental verification of timings on actual machines
where the code will be run, as this is an result that would not have
been expected from the models --- my speculation is that the cache
pre-fetch was sufficiently effective on this machine that the
additional memory demands of too-large a blocking size did not create
a bottleneck. In any case, the clever compiler, when allowed to
choose from a wide range of blocking values as expressed by a
qint parameter, can experimentally determine that it is safe to use
very large blocks. However, another machine which was also
i386-binary compatible, but with different latencies and bandwidths
for transfers between the cache and main memory, might well have
choked on the larger block values, hence it is desireable to set the
block size quasistatically and not statically.
32-bit integers take up 256KB of memory), we see that the
performance was hardly impacted at all when we moved to B=512. This
argues for experimental verification of timings on actual machines
where the code will be run, as this is an result that would not have
been expected from the models --- my speculation is that the cache
pre-fetch was sufficiently effective on this machine that the
additional memory demands of too-large a blocking size did not create
a bottleneck. In any case, the clever compiler, when allowed to
choose from a wide range of blocking values as expressed by a
qint parameter, can experimentally determine that it is safe to use
very large blocks. However, another machine which was also
i386-binary compatible, but with different latencies and bandwidths
for transfers between the cache and main memory, might well have
choked on the larger block values, hence it is desireable to set the
block size quasistatically and not statically.

