Learning a Visuomotor Map |
||
| Learning a Visuomotor Map MIT Artificial Intelligence Laboratory 545 Technology Square, #920 Cambridge, MA 02139 |
The ProblemThe problem that we would like to solve is this: given a point in visual space, how do we move the eyes to foveate on that point? For example, Cog is looking at the the end of its arm. Through some visual processing on the camera images, we determine that there is an interesting event happening at a point to the left and above the arm. What are the motor commands that are needed to move Cog's eyes so that the images are now centered on this interesting event? (This also has an advantage in that it brings the narrow-field cameras to foveate on this point which gives us much greater resolution to evaluate this interesting event).
Our ApproachWith the neck in a fixed position, this task simplifies to learning the mapping between image coordinates and the pan/tilt encoder coordinates of the eye motors. Initial experimentation revealed that for the wide-angle cameras, this saccade map became linear as you approached the image center but rapidly exploded near the edges. An on-line learning algorithm was implemented to incrementally update an initial estimate of the saccade map by comparing image correlations in a local field. This learning process, the saccade map trainer, optimized a look-up table that contained the pan and tilt encoder offsets needed to saccade to a given image coordinate. Saccade map training began with a linear estimate based on the range of the encoder limits (determined during calibration). For each learning trial, the saccade map trainer generated a random visual target location and recorded the normalized image intensities in a 16x16 patch around that point. The process then issued a saccade motor command using the current entries in the map. After allowing the camera images to stabilize, a local field around the center of the new image was normalized and correlated against the target image. Thus, for offsets (x,y), we sought to maximize the dot-product of the image vectors. Since each image was normalized, maximizing the dot product of the image vectors is identical to minimizing the angle between the two vectors. This normalization also gave the algorithm a better resistance to changes in background luminance as the camera moved. In our experiments, the offsets had a range of [-2, 2] in both dimensions. The offset pair that maximized the correlation was used as an error vector to the saccade map. Note that a single learning step of this algorithm does not find the optimal correlations across the entire image. The limited search radius vastly increases the speed of each learning trial at the expense of producing difficulties with local maxima. However, this simple strategy effectively exploited properties of the visual environment to provide a stable result. In the laboratory space that makes up Cog's visual world, there are many large objects that are constant over relatively large pixel areas. The hill-climbing algorithm exploited these consistencies. Our approach has the advantage that this algorithm can continue while other behaviors are active, so long as the eyes are moving. The process can run in the background and continually update our saccade map.
StatusTo allow other projects to continue on, a quick version of this algorithm was implemented. The simplified version has a saccade map that accounts for only the (x,y) image position and assumes that the head is centered on the horizontal meridian. To simplify the learning process, we initially trained the map with random visual positions that were multiples of ten in the ranges [10, 110] for pan and [20, 100] for tilt. By examining only a subset of the image points, we could quickly train a limited set of points which would bootstrap additional points. Examining image points closer to the periphery was also unnecessary since the field of view of the camera was greater than the range of the motors; thus there were points on the edges of the image that could be seen but could not be foveated regardless of the current eye position.
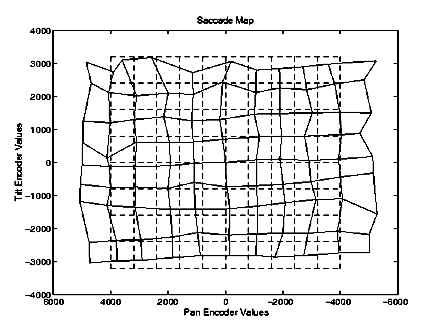
ResultsThe image below shows the data points in their initial linear approximation (dashed
lines) and the resulting map after 2000 learning trials (solid lines). The saccade map
after 2000 trials clearly indicates a slight counter-clockwise rotation of the mounting of
the camera, which was verified by examination of the hardware. The training quickly
reached a level of 1 pixel-error or less per trial within 2000 trials (approximately 20
trials per image location). Perhaps as a result of lens distortion effects, this error
level remained constant regardless of continued learning. FutureThe saccade map needs to be updated to account for the pan and tilt positions of the eyes. Additionally, better reporting of the results of the saccade map to other processes should be made available. These clips show Cog orienting its head and neck to a visual stimulus. The eyes are moving to look at moving objects in the field of view. Whenever the eyes move to their new target, the neck moves to point the head toward that same target. The first clip is from the new revision of Cog's head.
|
|
Representatives of the press who are interested in acquiring further information about the Cog project should contact Elizabeth Thomson, thomson@mit.edu, from the MIT News Office, http://web.mit.edu/newsoffice/www/ . |
||